Vectorial Color: visual materials for the oral presentation

Talk Itself Starts Here

Legacy Understanding

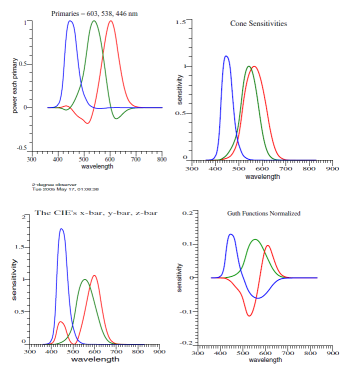
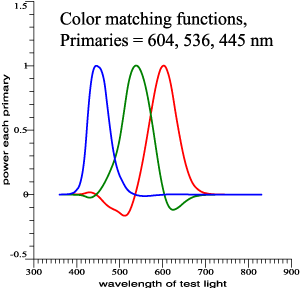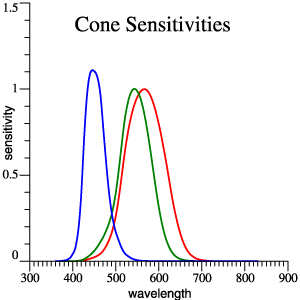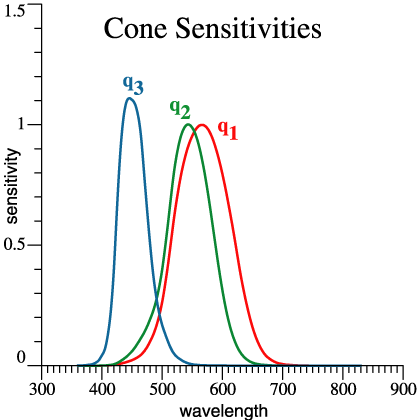
Fictitious but realistic color-matching data.			Cones, red, green and blue.
Traditional x-bar, y-bar, z-bar		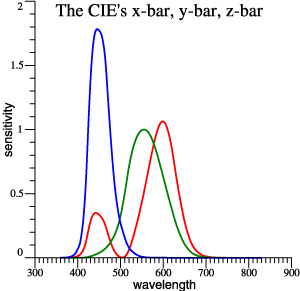	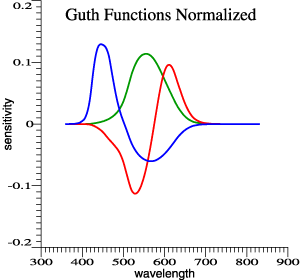Guth's 1980 model, normalized. Achromatic function is proportional to y-bar.
Linear transformations of color-matching data predict the same matches. This is Figure 1. < The only numbered figure! >

How does a set of 3 functions predict color matches?

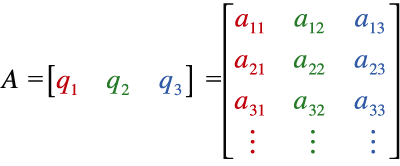	(Eq. 1)
A set of color matching functions, CMFs, can be thought of as column vectors, which become the columns of a matrix A. Matrix A can contain any of the 4 sets of color matching functions above, for example.

SPD as a Column Vector

The spectral power distribution of any light can be written as a column vector L₁. It is then summarized by a tristimulus vector V,

V = A^T L₁ . (2)

Light L₁ is a color match for light L₂ if

A^T L₁ = A^T L₂ . (3)

Refer again to the Figure 1. If Eq. (3) holds for one set of CMFs A, then it will hold for the other sets. That much is standard teaching.

4 lights that approximately match in color.

Moment of Reflection

So, everybody knows that alternate sets of functions can be equivalent for color-matching. But it's remarkable that 2 sets can be equivalent-for-matching, but also look very different, and be suited for other applications that go beyond matching.

For example:

The cone sensitivities relate to adaptation and constancy. It is often assumed that the 3 cone systems have separate gain settings. That leads to "von Kries adaptation," also known as the integrated reflectance model.
The simulated experimental data give clues about choosing primaries for additive color mixing, as noticed by Bill Thornton. (Explained below.)
The opponent model fits the intuitive idea that red and green are opposites, as are blue and yellow.

Nominal time = 1:37 pm, Pacific Time

Animation Digression: Simulated Experimental Data

Wavelength of the test light -->	The primary wavelengths are not unique, and the same facts can be presented in alternate sets of graphs, an awkward situation. However, Wright and Guild both used red, green, and blue primaries. The wavelengths are not really arbitrary. The mixing of 3 primaries models technologies such as television. Practical question: what wavelengths work best as primaries? More optical power was needed for Wright's red primary than for Guild's.
	Thornton found: The color matching functions tend to peak at certain fixed wavelengths, despite perturbation of the primaries. The peaks occur at the prime colors. Prime color primaries run the experiment at minimum power.
For the 2° Observer, the prime colors are 603, 538, and 446 nm. Since they are based on a minimum-power criterion, they are "prime" candidates for RGB video primaries, subject to further study. Important ideas reveal themselves at this linear stage, where color mixing is modeled by simple equations and graphs.

What's Missing?

	So... we have at least 4 interesting sets of functions that are equivalent-for-matching, but have further meanings. What's missing is a good scheme for vectorial addition of colors. In his 1970 Book, Tom Cornsweet emphasized vector addition to account for overlapping receptor sensitivities:
	My method is inspired by Cornsweet, but also by Jozef Cohen.

Jozef Cohen's Innovations.

Jozef B. Cohen's Book

Spectral reflectance can be measured at 100's of points across the visible domain, but for most objects the graph is smooth:

Smoothness of Object Spectral Reflectances

The smoothness of object colors is an underlying fact for color constancy, object metamerism,
and color rendering. In 1964, at the dawn of the computer age, Jozef Cohen used principal components analysis to find that a population of Munsell Colors could be modeled as a sum of 3 or 4 basis functions. [COHEN, JOZEF, “Dependency of the spectral reflectance curves of the Munsell color chips,” Psychonom. Sci. 1, 369-370 (1964).]

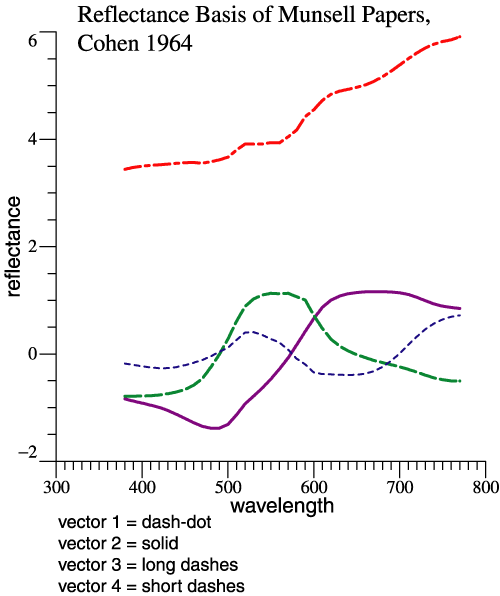The “Dependency” paper was little noted for 20 years, but is now widely cited. The idea is referred to as a “linear model,” and is the basis for many studies with a statistical flavor. Having used some linear algebra ideas in a curve-fitting task, Cohen then asked, “Could linear algebra be applied directly in thinking about color-matching data?” In the traditional presentation, color-matching data are transformed and one version is as good as another. Cohen asked a daring question: “Is there an invariant description for a colored light?”

We may well ask, “What would it even mean, that a function or vector is invariant?” Cohen started with Wyszecki’s idea of “metameric blacks.” If 2 lights have different SPDs, but are colorimetrically the same, they are metamers. Subtracting one light from the other gives a metameric black, a non-zero function with tristimulus vector = 0. Consider an example of D65 and a mixture of 3 LEDs adjusted to match:

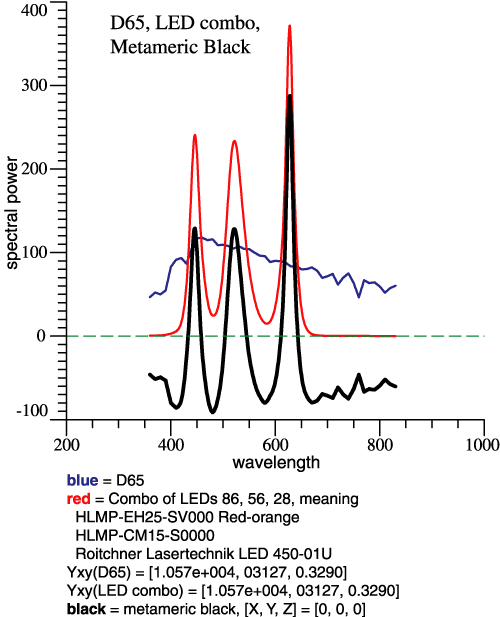The figure at left shows the concept of metameric black. A mixture of 3 LEDs matches D65. Subtracting D65 from the LED combo gives the black graph, a function that crosses zero and is colorimetrically black. The metameric black is a component that you cannot see, as noticed by Wyszecki. Cohen then said, “Let’s take a light (such as D65) and separate it into the component that you definitely can see, and a metameric black.” (My wording.) The component that you definitely can see is the light projected into the vector space of the color matching functions. Cohen called that component...

... ta-dah ...

01:44 pm, Pacific time

The Fundamental Metamer.

Cohen needed a formula to compute the fundamental metamer. As a practical matter, the “projection into the space of the CMFs” means a linear combination of CMFs that is a least-squares fit to the initial light. As on p. 3, let A be a matrix whose columns are a set of CMFs,
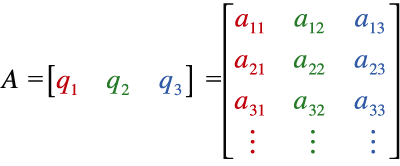	. (1)
For a light L(λ), we want to find the 3-vector of coefficients, C_3×1, such that L ≈ AC . (4) Where ‘≈’ symbolizes that least-squares fit. Today, you might do a web search and you would learn to solve for C using the Moore-Penrose pseudo-inverse = A⁺ = (A^TA)⁻¹A^T , so that (5) C = A⁺L = (A^TA)⁻¹A^T L . (6) That would give you C as a numeric 3-vector, and if we define ... Fundamental Metamer of L = L* = The least-squares fit to L, (7)

The Fundamental Metamer, continued.

then,

L* = AC . (8)

A numerical value for 3-vector C gives a numerical vector for L*, but no new insight. The value of C—the coefficients for a linear combination of CMFs—depends on which CMFs you are using. Nothing is invariant. Deriving everything from a blank page, Cohen in effect combined Eq. (6) and Eq. (8) to find that

L* = [A(A^TA)⁻¹A^T] L . (9)

Then L is the original light, L* is its fundamental metamer, and the expression in square brackets is projection matrix R:

R = A(A^TA)⁻¹A^T . (10)

Cohen noticed that R is invariant, and that led to other interesting ideas.

My algebra looks different from Cohen’s. But the invariant projection matrix R remains important. R is invariant in the strongest possible sense. If A is any set of equivalent CMFs, like any of the sets in Fig. 1, then R is the same large array of numbers, not scaled or transformed in any way. For proof, see Q&A.

Fundamental Metamer Example.

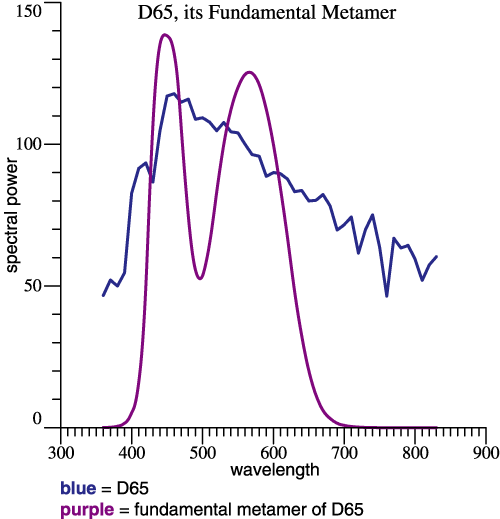At left for example, the blue curve shows L = D65. The purple curve is L*, the fundamental metamer of D65. The two curves are metamers in the ordinary sense. L*, a linear combination of CMFs, is found by:

L* = RL . (11)

Eqs. (8) and (11) have '=' and not '≈' because L* by definition is the least-squares approximation.

So that’s Jozef Cohen’s
Highly Original Contribution.

Now a few screens above,
We were talking about vectors...

Cohen References:
Cohen, Jozef, “Dependency of the spectral reflectance curves of the Munsell color chips,” Psychonom. Sci. 1, 369-370 (1964).

Cohen, Jozef, Visual Color and Color Mixture: The Fundamental Color Space, University of Illinois Press, Champaign, Illinois,
2001, 248 pp. <Book remains in print, as far as I know.>

1:50 pm, Pacific time

Orthonormal Opponent Color Matching Functions.

So, Cornsweet used vectors to deal with overlapping CMFs (a few screens above). Now we use that idea, but in a fancier way. To be consistent with Jozef Cohen’s discoveries, and enjoy other benefits, we can make color vectors by starting with Orthonormal Opponent Color Matching Functions :

The functions are easy to generate, or can be found at
http://www.jimworthey.com/orthobasis.txt .
I first generated them by applying Gram-Schmidt orthonormalization to Guth's 1980 functions.

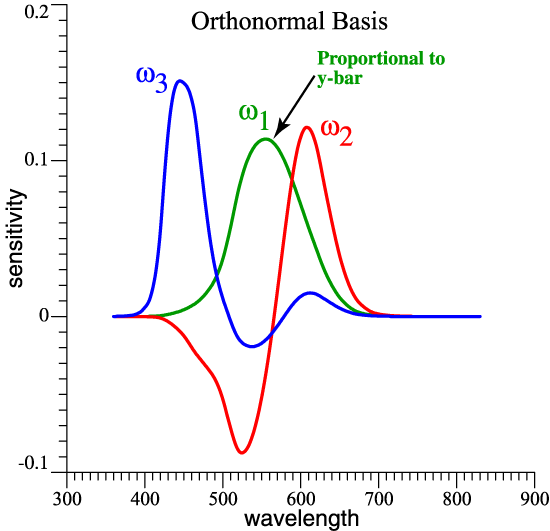
Orthonormal Opponent Color Matching Functions: Description.

Bra and Ket Notation

Working Class Summary

Although many clever ideas (from Cohen, Guth, Thornton, Buchsbaum, etc.) guided its development, in the end the orthonormal basis is not radically new:

ω₁ is proportional to old-fashioned y-bar (not shown). So ω₁ is not new.

ω₃ is similar to the old z-bar, which is essentially a blue cone function.

In the XYZ system, a non-intuitive feature is x-bar, an arbitrary magenta primary. It is replaced in the new system by ω₂ , a red-green opponent function. The opponent function confronts the overlap of cone sensitivities by finding a difference of red and green.

Let me say that again. An important feature of human vision is the overlapping sensitivities of the red and green cones. An opponent system confronts the issue of overlap. It re-mixes the red and green signals into ω₁ = red + green, and ω₂ = red - green.

Click to review graph of orthonormal basis
(Then use browser's back button.)

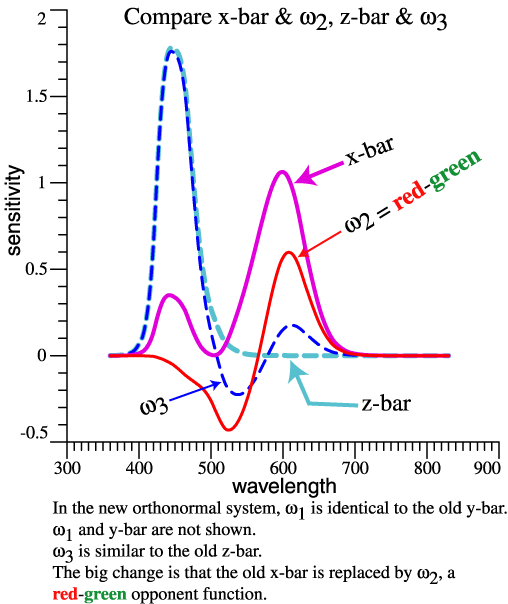Practicality

A new orthonormal basis could be created for any standard observer or camera. If it will suffice to have orthonormal opponent functions based on the 1931 2° Observer, then tabulated data are available at http://www.jimworthey.com/orthobasis.txt .

11
Orthonormal Color Matching Functions
James A. Worthey, Sat 2004 Oct 23, 20:57:46
1st column is wavelength in nanometers.
2nd column is omega-1 = achromatic
3rd column is omega-2 = red-green
4th column is omega-3 = blue-yellow
Put columns 2-4 in a big matrix called Omega.
If ' is matrix transpose, you can do this check:
Omega'*Omega = Identity Matrix (3x3) .
OTOH, Omega*Omega' gives Matrix R, the projection matrix.
First line of this file is the number of these comment lines!
360       4.457966e-007     -2.2732411e-007     5.19311685e-005
361     5.00036628e-007    -2.69438911e-007     5.83360809e-005
362     5.61041793e-007     -3.1959058e-007     6.55531511e-005
363     6.29616395e-007    -3.78213858e-007     7.36777575e-005
364     7.06564849e-007    -4.45743615e-007     8.28052783e-005
365     7.92691682e-007     -5.2261486e-007      9.3031092e-005
366     8.89228099e-007    -6.10848068e-007      0.000104556575
367     9.97816844e-007    -7.12879535e-007      0.000117585251
368     1.11987975e-006    -8.29715601e-007      0.000132215511
369     1.25683798e-006    -9.62361805e-007      0.000148545746
370     1.41011485e-006    -1.11182622e-006      0.000166674347
371     1.58042235e-006    -1.27658478e-006      0.000186520506
372     1.77058528e-006     -1.4627818e-006      0.000208614278
373     1.98519588e-006    -1.68299053e-006      0.000233970598
374     2.22884074e-006    -1.94971689e-006      0.000263604238
375     2.50611211e-006    -2.27561136e-006      0.000298530207
376     2.82701851e-006    -2.68023553e-006      0.000340414724
377     3.19139606e-006    -3.15714084e-006      0.000388841422
378     3.58857044e-006     -3.6799146e-006      0.000441701398
379     4.00786849e-006    -4.22203069e-006      0.000496885676
380     4.43861818e-006    -4.75688934e-006      0.000552285297

etc, etc. Recall that graphs are above.

Nominal time = 2:08 pm, Pacific Time

Fun with Matrices

Ω = [ ω₁ ω₂ ω₃ ] (12)
〈ω_i|ω_j〉 = δ_ij . (13)

Orthonormality, Eq. (13), can be expressed in matrix form:

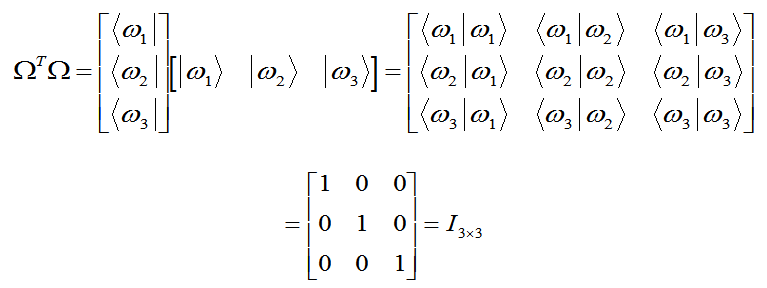(15)

or in short, Ω^TΩ = I_3×3 . (15)

If you multiply Ω and its transpose in the reverse order, you get a different interesting result:

ΩΩ^T = R . (16)

Eq. (16) is easily proved, but not right now. [Just substitute A = Ω in Eq. (10).]

Alternate Practical Presentation <Bonus item, not in handout!>

If you already have the functions x-bar, y-bar, and z-bar handy in your computer, then you can generate the orthonormal basis by adding and subtracting those vectors. It's one matrix multiplication.

If T is the 3×3 matrix below, and X is the array [x-bar y-bar z-bar] , then

Ω = X*T .

What's below is program output, where OB = OrthoBasis = Ω . The output explains a derivation for T and what's calculated numerically.

Abbreviate OB = OrthoBasis = Omega, and X = [x y z]-bar
We seek xfmn T such that OB = X*T. So, solve that equation for T:
OB = X*T
Multiply both sides by OB', then apply orthonormality:
OB' * OB = OB' * X * T
I = OB' * X * T
T = inv(OB' * X)             <transformation matrix that we need>
T = inv(OB'*X) =
{
[    0.0000000000 ,    0.1875633629 ,    0.0306246445 ]
[    0.1138107224 ,   -0.1332892909 ,   -0.0312159276 ]
[    0.0000000000 ,   -0.0397124415 ,    0.0793190892 ]
}
Now compute OB = X*T, and test the result:
OB'*OB =
{
[    1.0000000000 ,    0.0000000000 ,    0.0000000000 ]
[    0.0000000000 ,    1.0000000000 ,   -0.0000000000 ]
[    0.0000000000 ,   -0.0000000000 ,    1.0000000000 ]
}

Carrying plenty of digits gives a convincing identity matrix in the check calculation.

Graphing a Vector

Now recall Eq. (2) above, and let A = Ω . That is, let the set of CMFs be the orthonormal set. Then

V = Ω^T |L₁〉.

The ket notation is a reminder that |L₁〉 is a column vector.

A tristimulus vector V can be graphed in 3 dimensions. At left is the vector for a 603 nm narrow-band light at unit power. The vector length depends on the optical power of the light and the eye’s sensitivity at that wavelength. By definition,

V = [v₁ v₂ v₃]^T.

The vector is drawn from the origin. The achromatic (= white) v₁axis is the line from the origin that fades to white. Up-down is the red-green v₂ axis with red at the top. To the left from the origin is the v₃ or blue axis. The opposite of blue is yellow. The graph paper is colorized according to the color directions. The intuitive meaning of the opponent-color functions ω₁, ω₂, ω₃, leads to an intuitive graph.

5 Vectors

At left 5 colors are graphed:
Thornton’s Prime Colors, 603 nm, 538 nm, 446 nm, plotted at unit power, give long vectors. An extreme red, 650 nm, and a blue-green, 490 nm, also at unit power, give shorter vectors.

What is the significance of vector length?

The algebra of color vectors is specifically about additive color mixing.

5 Vectors Added

The same 5 vectors point from the origin, again for the 5 unit-power lights, at 603, 538, 446, 650, and 490 nm. Then the 5 vectors are added, tail to head, as vectors normally add. The resultant is a white vector.

So, vector length has a non-mysterious meaning:

According to the eye’s overlapping sensitivities, and a light’s wavelength and amplitude, each light maps to a vector with length and direction. Then vector addition predicts color matches.

Wavelengths of Strong Action

A color mixture is predicted by adding vectors, but vectors [X Y Z]^T are traditionally not graphed. Now suppose that it is 1950 and we are trying to invent color television. It will be helpful if the phosphor colors correspond to long vectors in well-separated directions. Indeed, the NTSC phosphors are approximately at Thornton’s Prime Colors, 603, 538, 446 nm.

Wavelengths of strong action in mixtures, nm.
2º Observer
longest vectors =	445	536	604
prime colors =	446	538	603
10º Observer
longest vectors =	445	535	600
prime colors =	445	536	600

nominal time, 2:08 pm, Pacific time

Locus of Unit Monochromats

If λ of a narrow-band light of unit power is stepped through the spectrum and then its color vector is plotted at each step, the vectors trace out a locus, shown at left. Jozef Cohen referred to this curve in 3 dimensions as "The Locus of Unit Monochromats."

The curve is a spectrum locus. By monochromat, Cohen meant a narrow-band light.

The word unit means unit-power. Each monochromat has the same optical power, which gives meaning to the vector lengths. The "unit power" idea was one of Cohen's great leaps forward, because in the legacy system, a vector [X Y Z]^T is found, and then we rush to plot it in the (x, y) diagram, losing the vector length. "Unit power" leads to a picture in which vector length has meaning.

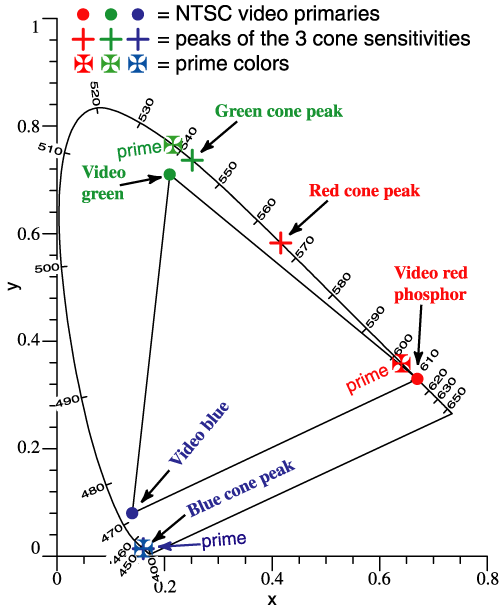Locus of Unit Monochromats (continued)

I often show the Locus of Unit Monochromats (LUM) by a surface. The locus is really the curve along the edge of the surface.

If you would look in Jozef Cohen’s articles, you would notice at first that his algebra looks different from mine. Also, he does not identify the LUM as a locus of tristimulus vectors. His vectors have more than 3 elements, and no preferred axes.

Cohen showed that the LUM as he described it has an invariant shape. The LUM based on the orthonormal opponent functions is the same invariant locus discovered by Cohen. Algebraic tinkering could rotate the LUM with respect to the axes, but its shape would not change (except for a possible mirror-image transformation).

To generate the LUM from the orthonormal basis, simply graph the rows of Ω.

5 Vectors Added (revisited)

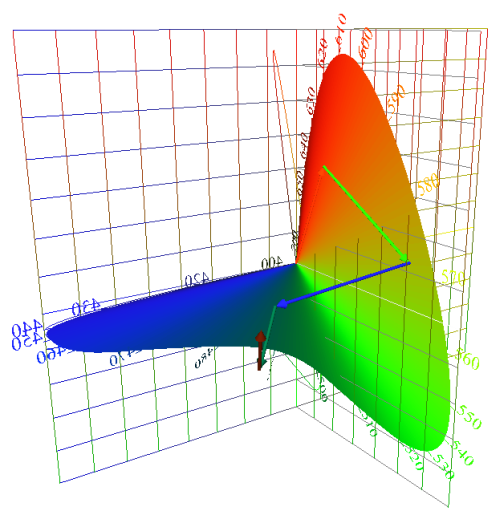The locus of unit monochromats can be included to give a frame of reference to a vector sum or other interesting diagram.

Composition of a White Light

The so-called "equal energy light" is one that has constant power per unit wavelength across the spectrum, indicated by a solid black line in the figure at the right.

The straight-line spectrum makes a simple discussion and is similar to a more realistic light, 5453 K blackbody (or 5500 if you like).

For the next step, let’s assume an equal-energy light that packs all of its power at the 10-nm points, 400, 410, and so forth, as indicated by the green dots.

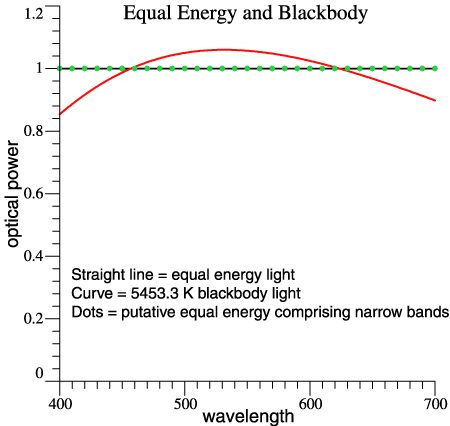Composition of a White Light (continued)

At right, the 31 narrow bands add up to make Equal Energy White. Each band contributes an arrow: blue, blue ..., blue-green, blue-green ... green ... green-yellow ... orange ... red. Added tail to head, the arrows sum to a particular white.

The resultant of all that vector addition can be graphed as a single arrow from the origin. Conceptually, that arrow has 3 components, also shown as white, red, and blue arrows. The one arrow, or the set of 3, those symbolize the traditional approach, except it would be done in XYZ space.

The chain of 31 arrows forms a pattern that will repeat for most white lights. It makes solid progress towards blue, then swings in the green direction, then back towards red.

Composition of a White Light (continued)

The swing toward red almost cancels the swing towards green. The greenish and reddish vectors are all present in the light, but red cancels green, approximately. I have explained the same idea in the past without vectors.

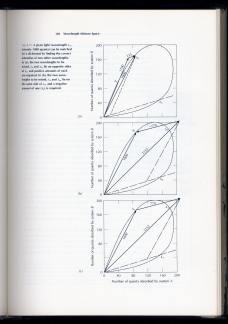
Now let this white light be shined on colored objects, and think of what an object color does. A red object reflects a range of the reddest vectors, while absorbing green and blue. The light looks white, but it must have red in it to reveal the red object as different from gray or green.

The most saturated colors will be those that reflect one or two segments of the spectrum and absorb the rest. You can think of those colors as "snipping out" a segment of the chain of vectors that compose the white light.

Is it a new idea to snip out part of the spectrum? No! The idea is called limit colors and is associated with MacAdam, Schrödinger and Brill, among others. On the next page is an illustration from MacAdam’s book, showing the possible ways to snip out parts of the spectrum. I won’t discuss limit colors at length, but they are a well-known idea.

nominal, 2:19 pm Portland time

Objects that Snip out Parts of a White Light

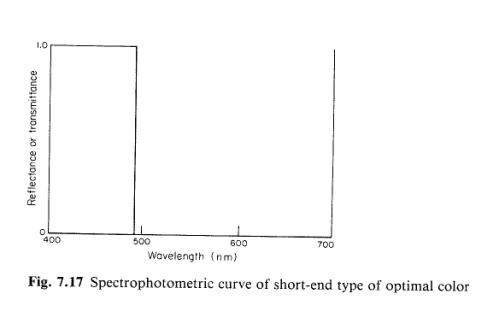Figures from D. L. MacAdam, Color Measurement: Theme and Variations, Springer, Berlin, 1981.
Observation: Many discussions of limit colors focus on a color gamut. Here we look at a more basic step, the limit color's interaction with the components of a white light.

Nominal time: 2:20 pm

One Example: a Short-end Optimal Color

At right, a hypothetical "short-end" color reflects all wavelengths up to 540 nm. The rest of the light disappears. The light source is the equal-energy light. Then the reflected light yields the vector chain on the right. The entire equal-energy spectrum, as above, would sum to the point where the one arrow, and the chain of three meet. When the full chain of vectors for the equal-energy light is shown, you can picture partial chains being snipped out according to MacAdam’s 4 types of optimal color:

short-end

long-end

middle

low-middle—meaning that short and long λ’s are reflected, but a band in the middle is not reflected.

We’ll revisit Composition of White Lights after a digression to more general issues.

Why So Many 3-Dimensional Drawings?

Why do I use so darned many of these 3-dimensional drawings? For detailed analysis and design, one might see a way to capture key information in a flat 2-D drawing. But the 3-D drawings have a

Special Charm.

If a person views some objects under a white light, then the eye and the light operate together. The eye and the light are both constant over the scene.

The chain of vectors in 3-D preserves all the information that colorimetry can give.

No assumption enters the chain of vectors in 3D. There are no preferred paint chips or anything like that.

Almost no simplification enters the drawings. If we stick to 10-nm steps, some tiny wiggles are lost, but conceptually—and in computer calculations—the smallest details can be used.

In short, the 3D picture makes no pre-judgment about what is important.

We can find even more uses for Cohen’s space.

Let’s look at another use of the orthonormal opponent functions.

Minimizing Correlation

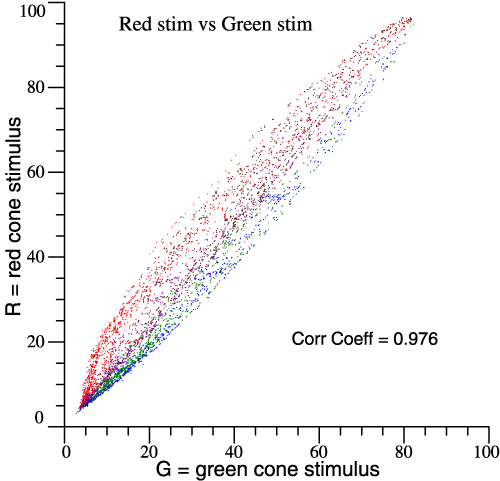
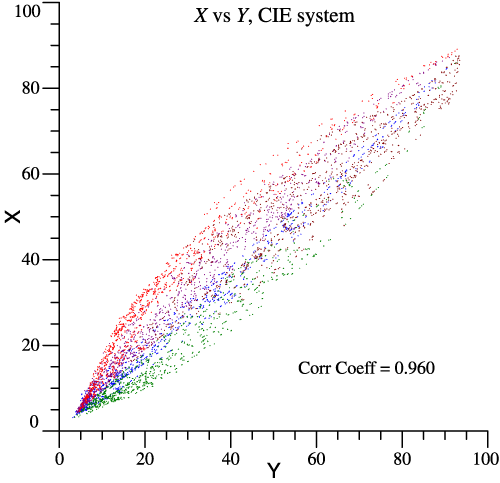
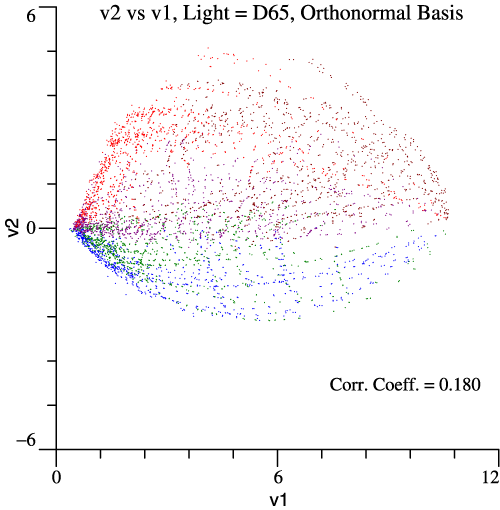
The orthonormal basis and Cohen’s space are a multi-purpose system. One benefit is that v₁, v₂, v₃ are less correlated than other sets of tristimulus values.

In metrology, it is easier to estimate propagation of errors if the starting variables are less correlated.

In information theory, if variable p is known, and q can be estimated from p, then q carries less information. The NTSC television standard uses opponent colors as a step in image compression, so the idea is not new.

Spectral reflectances are available for a set of 5572 paint chips: Antonio Garcia-Beltran, Juan L. Nieves, Javier Hernandez-Andres, Javier Romero, "Linear Bases for Spectral Reflectance Functions of Acrylic Paints," Color Res. Appl. 23(1):39-45, February 1998. Professor Garcia kindly sent me the raw data.

To make realistic visual stimuli, let the paint chips be illuminated by D65. Then one stimulus can be plotted against another to see if they are correlated or independent. Garcia et al. put the chips in color groups, so I’ve colored the dots accordingly. The graph above shows that red and green cone stimuli are highly correlated, correlation coefficient = 0.976. X vs Y in the legacy system is a little better, while the opponent stimuli v₁ and v₂ are most independent, Correlation Coefficient = 0.180 .

Relationships Among Equivalent Sets of CMFs

xfm_from_omega.pdf

Nominal time: 2:30 pm

CMFs Graphed as if they Were Lights

Because of orthonormality, the functions \|ω_j〉 plot to the v₁, v₂, v₃ axes. (Not emphasized in the drawing!) Legacy function y-bar also plots to the +v₁ axis. Red and green cones plot near to each other and to +v₁. Also, r cones and g cones lie in the v₁–v₂ plane. Blue cones and z-bar are the same direction and close to +v₃. x-bar is not in the v₁–v₂ plane, or on the spectrum locus. In short, the graph shows similarities and differences among functions.
Simplicity would be lost if a similar plot were made with axes X, Y, Z. Then, for example the y-bar function would not plot to the Y axis, since y-bar has non-zero inner products with x-bar and z-bar.

The orthonormal pairs, with cosine = 0, give the lowest correlation of the paint chips, but not zero correlation. With other populations of object colors, correlations may vary. Nominal time: 2:33 pm

Opponent Colors and Information Transmission

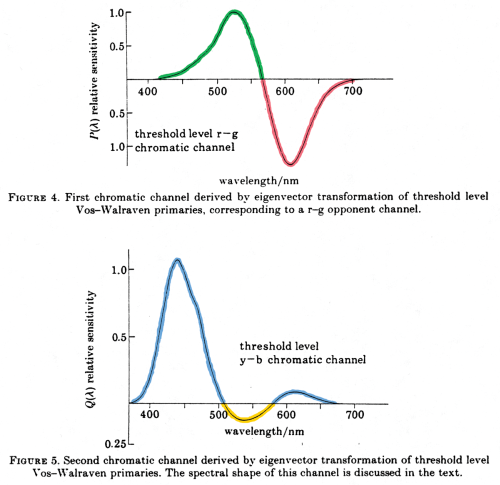
Above I’ve shown the benefit of an opponent system for information transmission (image compression) in an empirical way, by starting with thousands of paint chips. Buchsbaum and Gottschalk proceeded differently, deriving an opponent-color system to optimize information transmission. They started with cone functions that are similar to the ones I use, and got a result like my opponent model. That is, they got an achromatic function (not shown) similar to y-bar, and the red-green and blue-yellow functions shown at right. The achromatic and red-green functions have minimal blue input, and the blue-yellow function crosses the abscissa twice and looks very much like function that I have been using.
This equation, scanned right out of the original article shows how their first two functions have little blue input, etc:

Their functions A, P, Q are orthogonal, but not normalized. Long story short, Buchsbaum and Gottschalk started with cone functions and derived opponent functions. They had a specific goal of optimum information transmission. I derived opponent functions in a simple way and discovered their connection to Cohen’s work. In the end, the sets of functions are extremely similar, confirming that the opponent basis is appropriate for image compression and propagation-of-errors. All orthonormal sets based on the same cones lead to the same Locus of Unit Monochromats, so in that sense Buchsbaum’s set cannot be wrong. [Gershon Buchsbaum and A. Gottschalk, “Trichromacy, opponent colours coding and optimum colour information transmission in the retina,” Proc. R. Soc. Lond. B 220, 89-113 (1983).]

Value of Cohen's Space and Orthonormal Basis

Benefits of the orthonormal basis can be listed:

Makes nice spread-out vector diagrams. [Greatest separations possible.]
Opponent feature confronts the fact of red-green overlap.
Opponent feature gives meaning to the axes: whiteness, red-green, blue-yellow.
Gives decorrelated stimuli, good for image compression, and for propagation of errors.
Orthonormal functions lead to simple formulas such as Eq. (15) - (16) . [See Q&A items on “Fun with Orthonormal Functions,” and on "transform matrix."]
Using the orthonormal basis, and treating CMFs as lights, ω₁ plots to the v₁ axis, and so forth. By comparison, a non-orthogonal basis would lead to a crazy graph, where, e. g. x-bar would not plot to the X axis.

The last list item is most important and echoes Jozef Cohen’s ideas. If you have two lights (2 SPDs) as stimuli to vision, they have an intrinsic vector relationship. Each light has an invariant fundamental metamer, which is its projection into the vector space of the CMFs. Vectors V obtained using Ω have the same amplitudes and vector relationships as fundamental metamers. Functions x-bar and y-bar are intrinsically 40.5° apart, but ω₁, ω₂, ω₃ are 90° apart, so v₁, v₂, v₃ are more appropriate axes than X, Y, Z.

nominal time: 2:39 pm

End Digression, return to
Vector Composition of Lights

The figure at the right once again shows the equal energy light as a vector sum. Power is assumed to be in narrow bands at multiples of 10 nm, 400, 410, ... , 700 nm . Although the power is the same in all bands, they map to vectors of varying amplitude and direction, according to the facts of color matching. As a practical matter, the little vectors are based on certain rows of matrix Ω.	Equal Energy light as a vector sum.
	A key issue for lighting and color is that the chain of arrows swings toward green and back towards red. If this light shines on a white paper, the green and red almost cancel, but if it shines on a red pepper, the red pigment selects a group of red vectors, by absorbing green ones. Then it matters how much red was in the light.

Some Lights Have Less Red and Less Green

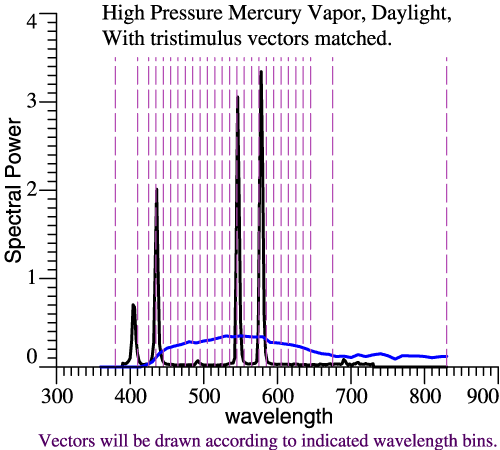
A white light has net redness or greenness that is small or zero. The same white point can be reached by different lights in different ways.

SPDs of 2 lights are plotted at right. The black line is High Pressure Mercury Vapor light, while the blue is JMW Daylight, adjusted to have the same tristimulus vector. (Yes, that means they are matched for illuminance and chromaticity.) The wavelength domain is chopped according to the dashed vertical lines. The wavelength bands are 10 nm, except at the ends of the spectrum, with most bands centered at multiples of 10 nm. If one light then multiplies the columns of Ω, those products could be graphed as a distorted LUM, but we skip that step.

Mercury light
spectrum and daylight spectrum.

Instead, the color composition of each light will be graphed as a chain of vectors. Nominal time = 2:42 pm

Comparing Color Composition of Lights

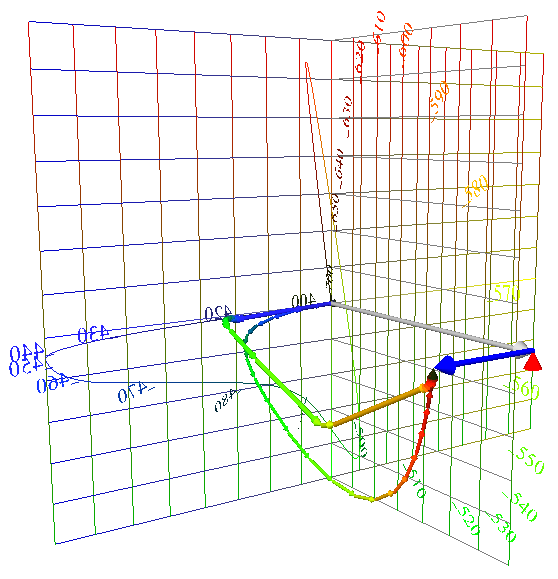
Now the same two lights are compared in their vector composition. The smooth chain of thin arrows shows the composition of daylight. Slightly thicker arrows show the mercury light. The mercury light radiates most of its power in a few narrow bands, leading to a few long arrows that leap toward the final white point. Compared to “natural daylight,” the mercury light makes a smaller swing towards green, and a smaller swing back towards red. Such a light would leave the red pepper starved for red light with which to express its redness.
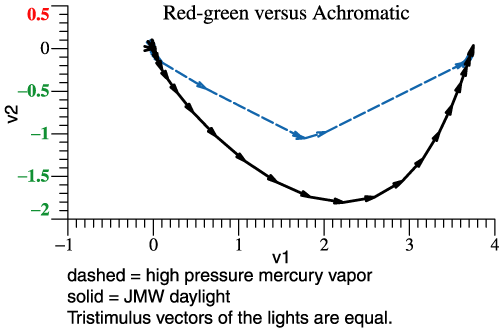
Above two lights are compared by the narrow-band components of their tristimulus vectors. At right the same information is shown, but projected into the v₁-v₂ plane. The loss of red-green contrast is the main issue with lights of “poor color rendering,” and that shows up in this flat graph. If you were really designing lights, you might use the v₁-v₂ projection as a main tool. You might want to add wavelength labels to the vectors. (In the VRML picture, λ info is indicated by coloration. In the picture at right, vectors that are approximately parallel pertain to the same band.)
Other interesting data can be plotted in Cohen’s space. Suppose that the 64 Munsell chips from Vrhel et al. are illuminated first by daylight and then by the mercury light. Since the mercury light lacks red and green, we expect it to create a general loss of red-green contrast among the 64 chips. The graph at right is a projection into the v2-v3 plane. Each arrow tail is the tristimulus vector of a paint chip under daylight. The arrowhead is the same chip under the mercury light. The lightest neutral paper is N9.5, and is a proxy for the lights. Notice that 3-vectors projected into a plane still have the properties of vectors in the 2D plane. As expected, red and green paint chips suffer a tremendous crash towards neutral.
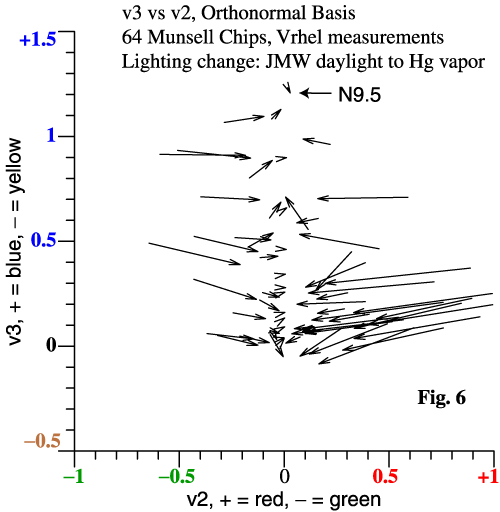Actual neutral papers appear as arrows of zero length. For an alternate presentation about comparing lights, please see “How White Light Works,” and the related graphical material.

Cameras and the "Luther Criterion"

The Luther Criterion, also known as the Maxwell-Ives Criterion:

For color fidelity, a camera’s spectral sensitivities must be
linear combinations of those for the eye.

For instance, in Fig. 1, (mini version at right), if one of the graphs represented a camera, it would meet the criterion.
On the other hand, it is less obvious how to describe a camera that departs from the ideal.
Some find a figure of merit, which disposes of the issue, but teaches little.
At CIC 14, Brill and I related the Luther Criterion to the Locus of Unit Monochromats, the LUM. We also brought Thornton’s prime colors into the picture and developed the ideas in many steps.
However, the poster itself presents a concise method for the actual calculation, “The Fit First Method.”
Now, assuming that we've covered the background pretty well, I’ll explain the Fit First Method in a few bold steps.

Bold Steps for Camera Analysis

The eventual goal is to make stimuli similar to the original scene. The Luther Criterion is a main issue, not incidental.
Color vision depends on the 3 cone sensitivities (or other color matching functions) taken together as a system.
The Locus of Unit Monochromats is an invariant 3D graph that summarizes color mixing by humans. It accounts for the 3 cone types as a system. (Any observer, but I use 2° Standard Observer.)
The camera has its own LUM. If the Luther Criterion is met, it will be the same as the human LUM.
By comparing the human and camera LUMs, we can relate the camera’s color-mixing properties to those of human, in detail.
There is one stumbling block. The LUMs may be similar or identical as shapes floating in space. To compare them, we need to rotate them into good alignment. The Fit First Method creates good alignment.

2:53 pm, Portland time

Compare Camera LUM to that of Human

At right is a screen grab from the virtual reality comparison of a Dalsa 575 sensor’s LUM to the 2° human observer LUM. The spheres represent the LUM of the camera The arrowheads trace the best fit to the human LUM by the camera functions.

Please let go of the details for a second, and try to see the big picture.

The human LUM is an invariant representation of trichromatic color vision. The camera has its own LUM. We want to compare them, but must somehow position them for a clear comparison. The Fit First Method finds the camera LUM in a good alignment.

The Fit First Method

Conceptually, the camera’s LUM (spheres) is more fundamental than the fit to the human LUM (arrowheads). The trick of the Fit First Method is to find the best fit first, then find the LUM from that. Here is the computer code: Rcam = RCohen(rgbSens) # 1 CamTemp = RcamOrthoBasis # 2 GramSchmidt(CamTemp, CamOmega) # 3 The camera’s 3 λ sensitivities are stored as the columns of array rgbSens . Because of the invariance of projection matrix R, it doesn’t matter how the functions are normalized, or whether they are actually in sequence r, g, b. Statement 1 finds Rcam, the projection matrix R for the camera. RCohen() is a small function, but conceptually, RCohen(A) = Ainv(A’A)A’ . (7) In other words, step 1 applies Cohen’s formula for the projection matrix. Then Rcam is the projection matrix for the camera. In step 2, the columns of OrthoBasis are the human orthonormal basis, Ω . The matrix product Rcam*OrthoBasis finds the projection of the human basis into the vector space of the camera. But, the wording about projection is another way of saying that step 2 finds the best fit to each ω_i by a linear combination of the camera functions. So, step 2 is the “fit” step. (More programming specifics.)
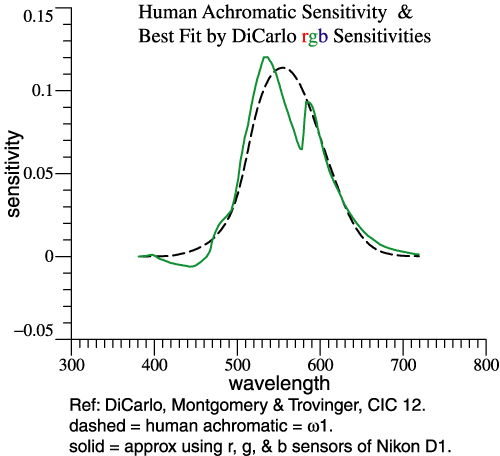
Step 2 does 3 fits at once, but let's look at just one. At right, the dashed curve is ω₁, the human achromatic function. The camera in question happens to be a Nikon D1. The solid curve is a linear combination of that camera’s r, g, and b functions that is the least-squares best fit to ω₁. There would be other ways to solve the curve-fitting problem, but projection matrix R is convenient. A best fit is found for each ω_j separately. The resulting re-mixed camera functions are not an orthonormal set.
Step 3, Orthonormalize the Re-mixed Camera Functions
Since the re-mixed camera functions are computed separately, they are not orthonormal and would not combine to map out a true Locus of Unit Monochromats. But they mimic Ω and are in the right sequence. We need to make them orthonormal, which is what the Gram-Schmidt method does, Step 3.

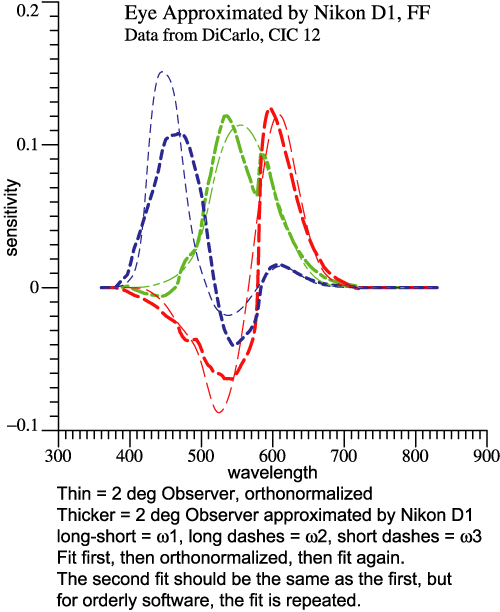
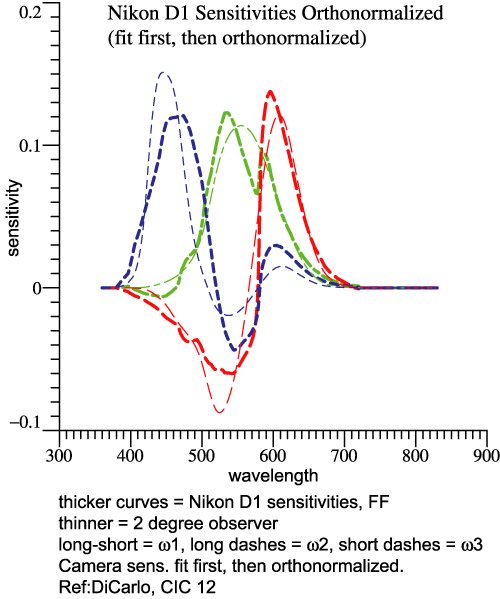
The two sets of graphs above look similar. But the one on the left shows the set of “fit” functions. The one on the right shows the orthonormal basis of the Nikon D1. The thinner curves pertain to the 2° observer, the thicker ones to the camera. Why Does it Matter? When you have the orthonormal basis, for the eye or for a camera, you can do many things with it. Combining the 3 functions generates the Locus of Unit Monochromats. The orthonormal property leads to some simple derivations. On the Q&A page, see "Can we have fun with orthonormal functions?" The Noise Issue To extract color information, some subtraction must be done. The signals subtract but the noise adds (in quadrature). The noise discussion becomes more concrete when one can say exactly what subtraction will be done. The camera’s orthonormal basis is a natural to be the canonical transformed sensitivity. Orthogonality means “no redundancy” and normalization standardizes the amplitude. There’s a numerical noise example worked out in the CIC 14 article. For now, the point is that expressing camera sensitivities as an orthonormal basis is a giant step towards dealing with noise.

3:02 pm, Pacific time

Camera Example, Nikon D1

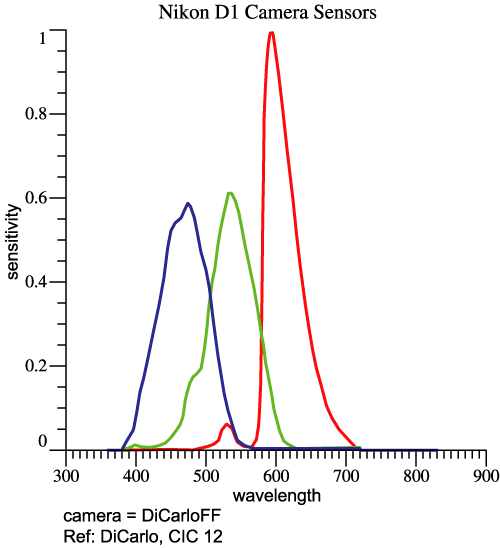
The last 4 graphs above pertained to the Nikon D1, based on data from CIC 12. At right are the camera’s red, green, and blue sensitivities. The camera’s LUM can be compared to the eye’s. Rather than another perspective picture, we now view the LUMs in orthographic projection (2 graphs below). The dashed curves are the human locus. The solid curves are the camera’s locus, while the tips of the small green arrows are points on the best-fit sensitivity function.

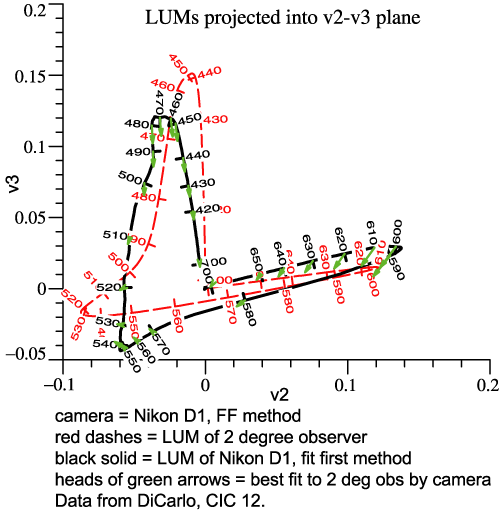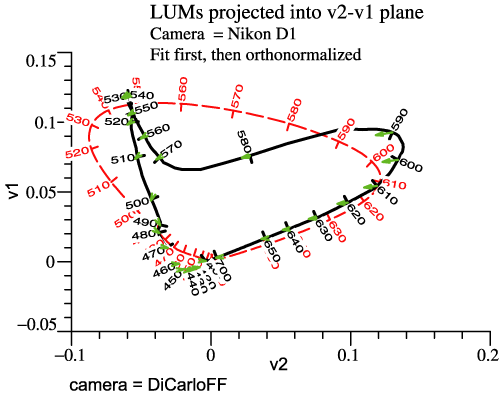
Now you may say “These curves mean nothing to me!” That may be at first, but the graphs contain a complete description of the camera sensor, with no hidden assumptions, and no information discarded. Finding Some Meaning in the Camera's LUM Consider the left-hand graph, “LUMs projected into v2-v1 plane.” Only the red and green receptors contribute to the human LUM in this view, and v1 is the achromatic dimension for human, based on good old y-bar. In this plane at least, the particular camera tends to confuse wavelengths in the interval 510 to 560 nm, which are nicely spread out as stimuli for human. Yellows, say 560 to 580 nm, have lower whiteness than they would for human. The camera has other differences from human that may be harder to verbalize. To the extent that finished photos look wrong, one could revisit these graphs for insight. More Examples Five detailed examples were prepared in 2006, and they are linked from the further examples page. For instance, Quan’s optimal sensor set indeed looks good in any of the graphical comparisons to 2° observer. (See http://www.cis.rit.edu/mcsl/research/PDFs/Quan.pdf .)

Something Completely Different: a 4-band Array

Nominal time: 3:08 pm

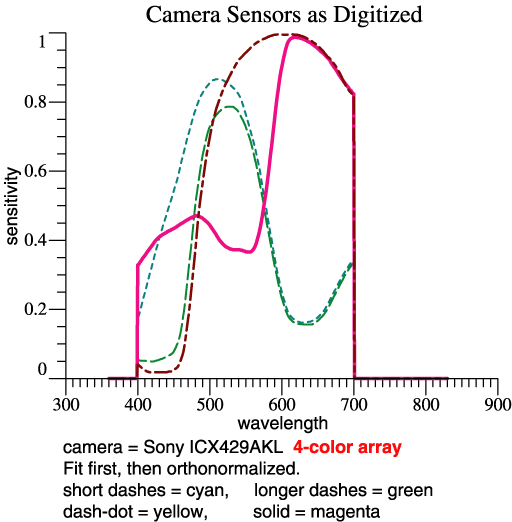
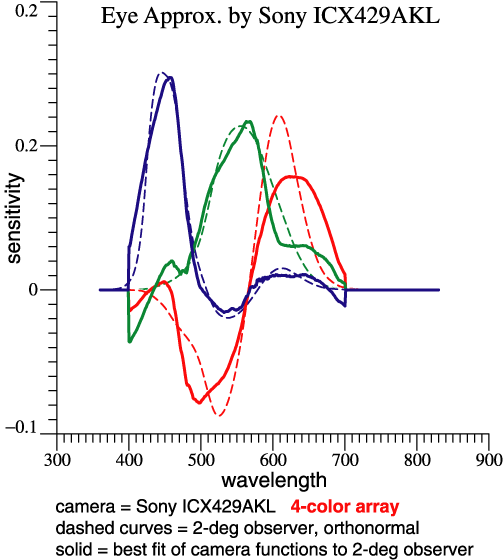
Sony publishes a specification for a 4-band sensor array, the ICX429AKL. I’m not sure of the intended application, but it could potentially be applied in a normal trichromatic camera. The Fit First Method readily fits the 4 sensors to the 3-function orthonormal basis.
The four sensitivities are seen at right. The key steps look the same: Rcam = RCohen(rgbSens) CamTemp = Rcam*OrthoBasis GramSchmidt(CamTemp, CamOmega) . Recall that the projection matrix Rcam is a big square matrix of dimension NxN, where N is the number of wavelengths, which might be 471. The 4th sensor adds a column to the array rgbSens, but does not change the dimensions of the result Rcam. 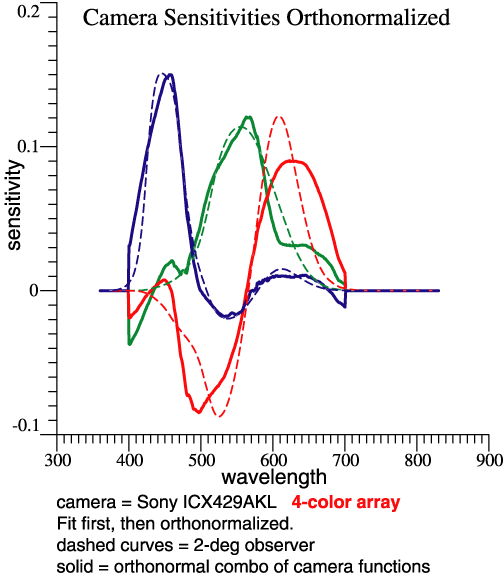After the key "fit first" steps, I did have to re-think some auxiliary calculations because of the 4-column sensor matrix.
The camera's orthonormal basis Rcam comprises 3 vectors that are linear combinations of the 4 vectors in rgbSens. I wanted to find the 4x3 transformation matrix relating the one to the other, in order to stimulate thinking about noise. The program output itself explains the method as follows: Similar to Eqs. 15-18 in CIC 14 paper, Transform from sensors to CamOmega: We want to solve CamOmega = rgbSens * Y , where Y is coeffs for 3 lin. combs. MPP = inv(rgbSens'rgbSens) rgbSens' Y = MPP*CamOmega = 0.24845 0.13737 0.35971 -0.34663 -0.43708 -0.45585 -0.22433 -0.088434 -0.033503 0.26839 0.22522 0.055984 Column amplitudes = vector lgth of each column = 0.55158 0.51812 0.58433 The columns of rgbSens actually contain the 4 sensitivities, cyan, green, yellow, magenta. MPP is the Moore-Penrose Pseudoinverse. (See Wikipedia and pp. 9-10 in "notes.") Keeping in mind that the sensitivities are all >= 0, matrix Y gives some idea how much subtraction is done to produce the sensor chip’s orthonormal basis. That’s a step toward thinking about noise. Below are the 3 orthonormal functions, and also the 3 best-fit functions made from the 4 camera sensitivities. The only source of “noise” is the errors that I introduced while converting graphs to numbers. It becomes more visible here, after subtractions.

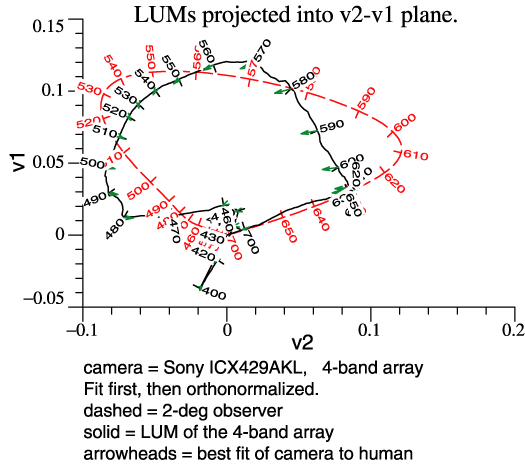
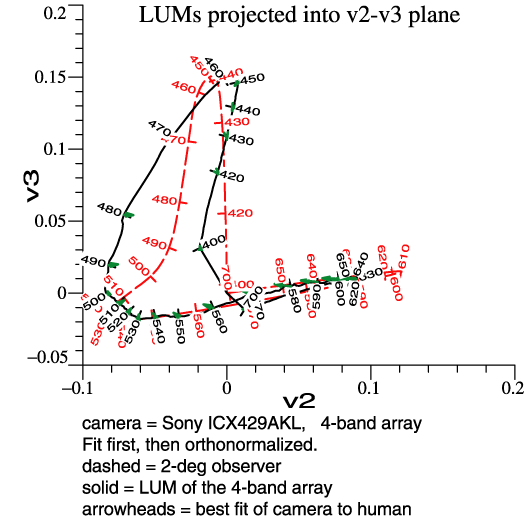
Some noise also shows up in the projections of the LUM, below. It would appear that color fidelity is not good; reds and oranges may lose some redness.

3:15 pm

Combining LEDs to Make a White Light?

In the 1970s, William A. Thornton asked an interesting question: If you would make a white light from 3 narrow bands, how would the choice of wavelengths affect vision of object colors under the light? His research led to the Prime Colors, a set of wavelengths that reveal colors well. From that start, he invented 3-band lamps and was named Inventor of the Year in 1979. 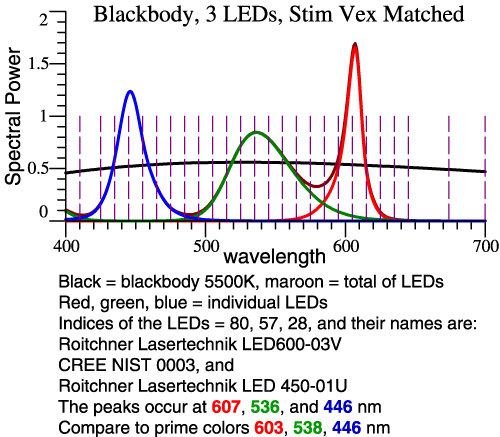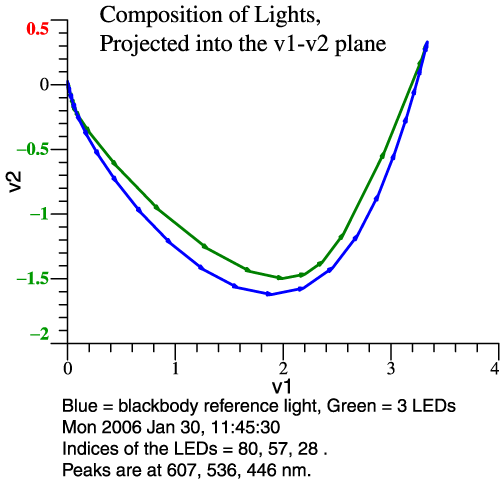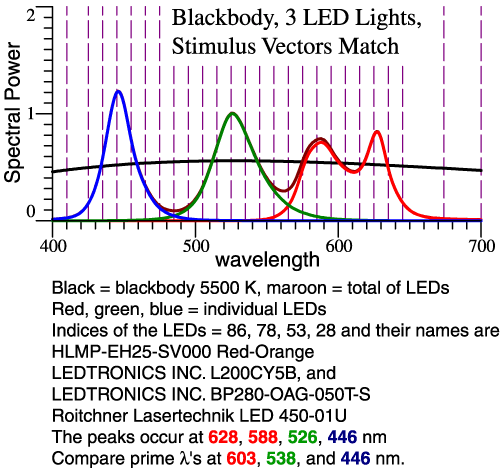He continued his research and made the definition of prime colors more precise. Problem Statement: For the 2° Observer, Thornton’s Prime Colors are 603, 538, 446 nm. [See CIC 6, and Michael H. Brill and James A. Worthey, "Color Matching Functions When One Primary Wavelength is Changed," Color Research and Application, 32(1):22-24 (2007). Also see Wavelengths of Strong Action, above.] If you would make a light with 3 narrow bands at those wavelengths, the light would tend to enhance red-green contrasts, making some colors more vivid, though it would do a bad job with saturated red objects. You might think then that a white light could be made from 3 LEDs whose SPDs peak at those wavelengths. This idea falls short because LEDs are not narrow-band lights. Our task then is to see what happens when real LEDs are combined, and design a good combination by speedy trial-and-error. We'll see two graphs per example: the LED spectra and their sum, and then the vectorial composition of the LED light in comparison to 5500 K blackbody. Clicking either image gives more detailed information. Example 1: Let LED Peaks ≈ Prime Colors The reference white is 5500 Kelvin blackbody. From 119 types measured by Irena Fryc, 3 LEDs are chosen by their peak wavelengths, as shown at left. Then we see at right that the blackbody (blue line) makes a bigger swing to green and back. This LED combo will dull most reds and greens.

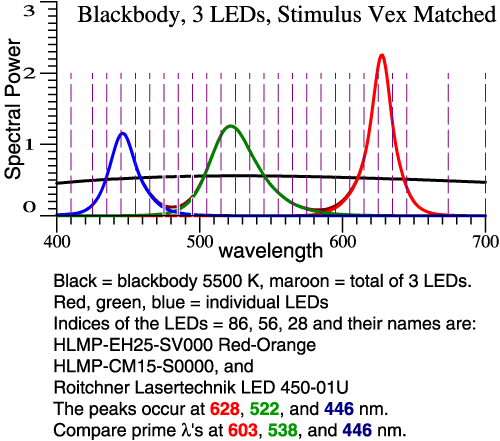
Example 2: Greener Green and Redder Red To increase the swing towards green and back, we let the green be greener (shorter λ) and the red be redder (longer λ). In all cases, the LED amplitudes are adjusted so the total tristimulus vector matches the blackbody.

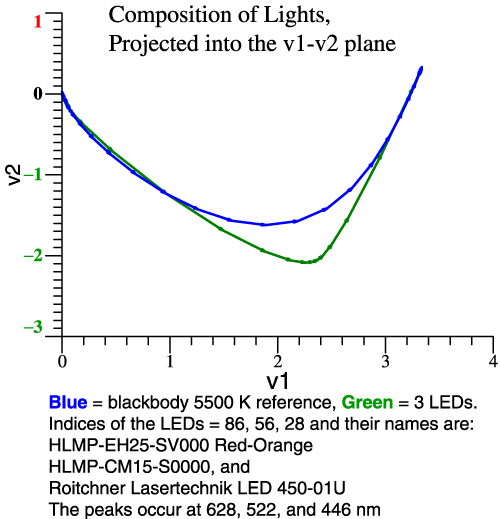Still on example 2, we can see from the vector composition (right-hand graph) that red-green contrast will be good, but some colors may be particularly distorted. Clicking the left-hand graph confirms that idea in the color shifts of the 64 Munsell papers. Example 3: Broaden the Red Peak The problem in example 2 is known to some lighting experts. The light needs to have a broader range of reds. The remedy is to use 2 red LEDs. For simplicity, the proportion of the 2 reds is fixed, not adjustable.

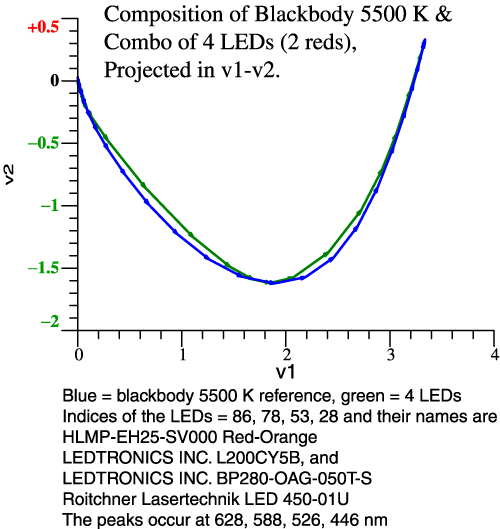Think of those green and red limit colors. Some of those colors will still be dulled, but we are tracking the blackbody pretty close. Further tweaking is possible.

3:22 pm

Vectorial Color

Sets of functions can be equivalent for color matching, but look different, and have other meanings, such as cone sensitivities or opponent functions, Fig. 1. This great insight is part of our legacy from the 20th century and earlier.
But, which color matching functions are best for graphing color vectors? There is no 20th-century answer, but you can take Guth’s 1980 functions, and orthonormalize them, and that will work. That’s the orthonormal basis.
Jozef Cohen noticed that colors have intrinsic vector relationships. His work led to the invariant Locus of Unit Monochromats.
In its original use, Cohen’s projection matrix R takes any spectral power distribution and finds a metamer that is a linear combination of the color matching functions used to make R.
More generally, R can be used to fit any function by a linear combination of functions. Using R in this way leads to the 3-step Fit First Method for finding a camera’s Locus of Unit Monochromats.
We have analyzed lights and cameras. The graphical methods tend to preserve details, not lose them.
Matrix R and the orthonormal basis lead to interesting algebraic methods. See the Q&A page.
In making vector diagrams, you'll find that you must adjust a vector length, or adjust two vectors to match, and so forth. If those steps feel unfamiliar, it's because traditional methods tend to discard the amplitude of color vectors.

Invariants

My numbers and graphs are based on the 2º observer. If a different standard observer were used, details could change, but certain basic ideas would not change:

The formula for R:

R = A(A^TA)^-1A^T . (10)

The fact that R is always the same numerical array, for a given observer.
The relationship of R to the orthonormal basis:

Ω^TΩ = I_3×3 . (15)
ΩΩ^T = R . (16)

The LUM for the 2º observer, including the wavelengths of the longest vectors. Plotting the rows of Ω draws the LUM. A different orthonormal basis for the 2º observer will draw the same LUM.
The fact of red-green overlap, and the implication that a light can be deficient in red and deficient in green.
The idea that a camera has an LUM, and if its LUM is the same as the eye’s, then the camera meets the Luther criterion.

If vectorial color is forgotten and then re-invented in 50 years, these ideas will come out the same. They transcend the personalities of those who discovered them.

Food for Thought ...

Vectorial Color Is About Color Mixing.
It Is Not About Any Neural Processing, Only Transduction.

Cohen’s ideas relate to making best use of color mixing data. The orthonormal CMFs are a convenient way to map stimuli into Cohen’s space. They are not a hypothesis about retinal wiring.

We have also seen that "mere" color mixing—the linear stage of vision—is the key to understanding color rendering and color camera sensors.

The End

Thank you very much for signing up and for your attention.

Please feel free to contact me at any time. I am always

eager to discuss lighting, color, cameras etc.

Jim Worthey

www.jimworthey.com

Nominal: 3:30 pm

Special Credit

William A. Thornton
Jozef B. Cohen

Michael H. Brill
Tom Cornsweet (1970 Book)
Ronald W. Everson (taught color fundamentals)
David MacAdam and Gershon Buchsbaum who mentioned orthogonal color matching functions.

(But MacAdam gets a demerit for disparaging Cohen's work.)

Calculations were done with O-matrix software.

William A. Thornton
1923-2006

Jozef B. Cohen
1921-1995

Bonus Picture: Jim Worthey, Jozef Cohen, Nick Worthey, circa 1993
Jim, Jozef, Nick

Lighting for a Copy Machine??

In 2007, I promised to combine the camera analysis and the lighting analysis, to analyze something like a copy machine, where the sensors and the lighting are under engineering control. In 2008, I did not make that promise. This is now a bonus section. It gets confusing because there are 2 independent variables, the light and the sensors. It will be assumed that the copy machine uses a combination of LEDs for a light. Then the copier discussion is a continuation of the LED discussion above.

So, We Know How to Design a Light.
Now Let the Camera Also be a Variable.

Let the lights be the last pair demonstrated above. The reference white is 5500 K blackbody. The 2 red LEDs are in fixed proportion, but the R, G, and B LEDs are adjusted to match the blackbody. The adjustment of R, G, B is done for human, and then separately for the camera. Using the Fit First method, it is possible to graph the human and camera sensitivities together, and then the compositions of the lights as seen by human and by camera.

Analysis of a (Very Hypothetical) Color Copier
The same LEDs are used as in the final light design above, p. 62. The camera is the Nikon D1, whose sensitivities are given on page 52. The data were borrowed from DiCarlo’s paper at CIC 12. (Page numbers refer to the tutorial handout.)
A Different Hypothetical Copier
Now the light is the same, but the camera is the “optimal” sensor, taken from Quan’s dissertation. The camera’s total “reach” into the green and back towards red is like the eye’s. But, many reds and greens will be dulled. You can see it by thinking of them as pass-band colors. The camera falls short because parts of the chain of vectors are too straight. To this camera, successive bands point in the same direction in color space, at least in this projection. We can see the same thing by looking at the Quan sensor’s Locus of Unit Monochromats, next graph. To the extent that a camera fails to discriminate certain wavelengths, the light can't fix the problem.
At right, the LUM of the Quan Sensor is compared to that of human. This sensor is better than many; It tracks the human LUM in a general way. We can see shortcomings in two areas. Picture the “unit monochromats,” the vectors that define the curves. The human vectors have steadily changing direction but long amplitude, from about 540 nm to 605 nm. Then the human LUM goes smoothly round the bend, but there is still some change of direction at 610, 620, 630 nm.
By contrast, the Quan sensor goes round the bend too soon, at 585. In a second quirk, the Quan sensor tends to lump together 520, 530, 540, 550, wavelengths that would be well discriminated by human. These features of the Quan LUM translate into the too-straight regions when lights are composed on p. 56. The lumping-together of wavelengths around 540 is something that many cameras do, and it happens because the red sensitivity is negligible there. The Quan sensor does discriminate those wavelengths along the v3 or blue-yellow dimension. There is no way to fix the lumping-together by changing the light. At the long-wavelength end, it might be possible to get some marginal improvement by boosting the light at long wavelengths, since the issue is a kind of absolute sensitivity dropoff.

Bonus Example: Multi-primary System (N > 3)

This example is based on real hardware. A laser radiates in 8 narrow bands at once, 647, 568, 530, 520, 514, 488, 476, and 457 nm. Using an acousto-optic modulator, it is possible to modulate the 8 bands separately. I was asked a question about how to program the gadget, but a more basic question is, "What do you really have colorimetrically?" A red, a green, and a blue would give a good range of video colors and then what can the other laser lines contribute?

Each of the lines has an intrinsic power limit, and then according to the wavelength and the eye's LUM, a color vector results. For instance, we know that long-wavelength red makes a nice ruby color, but the eye's sensitivity is declining at the longest wavelengths. Those facts are expressed in the vector diagram, not lost.

Multi-primary
system, 8 laser wavelengths

In the diagram above, the wavelengths with their power limitations give vectors from the origin. Then those vectors are scaled down by a convenient ratio and added to give the total vector of the unmodulated laser. The 647 nm is a nice ruby red. The 514 nm line can be a good saturated green primary, then there is a question whether the 530 nm line adds much. A final design would depend on goals, including needed power level. The point for now is that the vector diagram combines colorimetry with the physical data in a logical way.

Stop

Scroll No Farther

Material Below Addresses Obscure Questions

Spectrum Locus for 4 Different Sets of Color Matching Functions

Orthonormal Basis Functions (Graph as Cohen drew it.)	Color Matching functions similar to Raw Experimental Data
Cone sensitivities, r, g, b	CIE's x-bar, y-bar, z-bar

"Boomerang Graph," Not a Chromaticity Plot