|
1
|
Lighting has a purpose,
which is to render object properties into black-white and color
contrasts. Black-white rendering tends to be in the artistic
vocabulary, while color rendering is treated as a nuisance engineering
issue. The idea that both kinds of rendering are quantifiable and part
of the basic functionality of lighting is at odds with the hidden
assumptions that many people make. |
|
|
2
|
Objects that are shiny or
transparent image the contrasts of their environment. While this is
well understood in computer graphics circles, it is seldom acknowledged
in the lighting discussion. |
|
|
3
|
Everyday speech puts
trust in the light and does not acknowledge its role. A purpose of
these articles is to ask the question, to find the right words to talk
about color rendering. |
|
|
4
|
The focus is on the
linear, physical, interaction of the object, the light, and the eye. My
approach is that of a physicist or lighting inventor who is interested
in the "inner workings" of things. |
|
|
5
|
"Color rendering"
includes loss or gain of chroma. Some in the lighting industry have
understood that "poor color rendering" usually equates to "dull
colors," but the issue is seldom stated in clear language (apart from
my prior work). |
 |
| 6 |
When chroma is lost in a
systematic way, so is color contrast. |
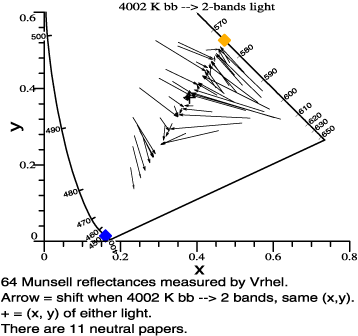
| 7 |
The two-band light is a
prototype for bad color rendering. Thornton and others have noted this
fact, but it remains as a simple insight that is seldom mentioned.
Render Ask, Fig. 1, shows a detailed example. |
|
|
8
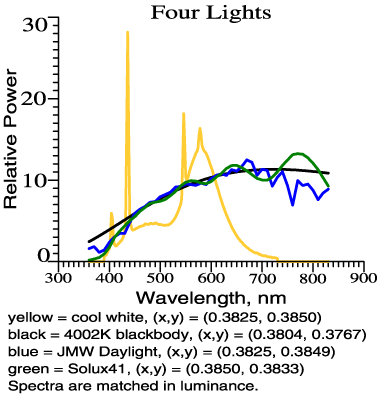
|
The practical reality of
color rendering is illustrated by a comparison of four lights that are
equated for illuminance, and approximately equated for chromaticity,
Render Ask, Fig. 2. |
 |
|
|
9
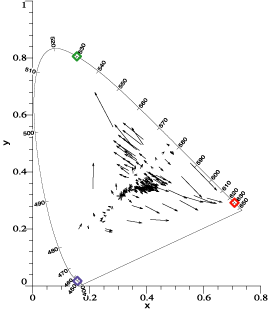
|
Within the apparatus and
experimental design of the famous Quantitative Retinex Experiment is a
color rendering example. |
 |
|
|
10
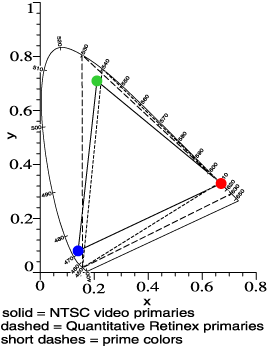
|
In the universe of color
technologies, lighting is similar to television. |
 |
|
|
11
|
Thornton's Prime Color
ideas can be approximately explained in terms of an opponent color
theory. |
 |
|
|
12
|
The reader is reminded of
the connection between prime colors and the diagonal of Matrix R. Jozef
Cohen did point out this relationship. |
|
|
13
|
Neodymium glass offers a
critical test of Thornton's Prime Color theory. |
|
|
14
|
Color Rendering and
Object Metamerism are separate issues. While I believe that this
distinction was seen intuitively by past experts including the original
authors of the Color Rendering Index, it is sometimes overlooked. |
|
|
15
|
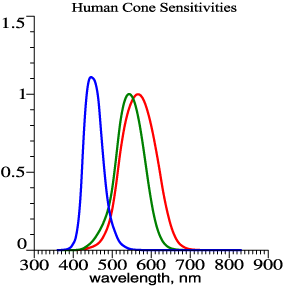
What permits the
two-bands light to be seen as white is the great overlap in spectral
sensitivities of the red and green receptors. (Going beyond what is
said in the color rendering articles, it seems clear that Bill
Thornton's Prime Colors, and Jozef Cohen's Matrix R are both methods
for dealing with the overlap of red and green sensitivities. Jozef
Cohen wrote about "the structure of color space." If the color
receptors had three narrow-band and non-overlapping sensitivities,
those sensitivities would jump out of color-matching data. The
sensitivities would be orthogonal functions with little need for
transformation of primaries, opponent color models, Matrix R or Prime
Colors.) |
 |
|
|
16
|
Guth's opponent model has
practical utility because of its simplicity. Opponent colors as a
method for color engineering was used in the invention of color
television. |
 |
|
|
17
|
Since opponent-color
sensitivities look like orthogonal functions, it might be useful to
orthogonalize them. |
|
|
18
|
Color matching functions
can be used as basis functions of spectral reflectance. Jozef Cohen
made this innovation, but it is taken a little further here. |
|
|
19
|
The new color rendering
model predicts colorimetric shifts. The numbers that make the
prediction are the same numbers that can be used for overall assessment
of a lighting substitution. |
|
|
20
|
Within the color
rendering model, objects are characterized by their tristimulus values
under a pivotal light. The pivotal light can very well be some familiar
light such as D65 (6500 K daylight). Therefore, the model incorporates
the familiar assumption that if you know an object's tristimulus value
under D65, you know a lot about the object. |
|
|
21
|
Thanks to the
opponent-color formulation, the illuminant change is represented by a
matrix whose elements have intuitive meaning. |
|
|
22
|
The smoothness assumption
is used explicitly in deriving the color rendering method. |
|
|
23
|
The opponent-color basis
functions are made orthonormal, with an added feature. They are
orthonormal with the pivotal light as a weighting function. |
|
|
24
|
Bra and ket notation is
used to emphasize the role of inner products and orthogonal functions. |
|
|
25
|
The traditional CRI
emphasized summing up the vector magnitudes of colorimetric shifts. By
looking at the inner workings (idea 4 above), we see that even if the
colorimetric shifts are graphed, the CRI's pastel chips give a
non-revealing result. It is saturated reds and greens that are in
greatest jeopardy from poor color rendering. |
|
|
26
|
Figs. 5 and 6 of Render
Calc permit a grand comparison of many diverse lights in a way that
speaks to the need for red-green and blue-yellow contrasts. |
|
|
27
|
The neodymium-filtered
light stands out because it enhances both red-green and blue-yellow
contrasts, relative to the same source without the filter. |
|
|
28
|
An explicit challenge to
the usual lighting discussion: "lighting discussions often operate on
the peculiar assumption that what is most obvious need not be studied." |
|
|
29
|
Some common lighting
systems cause stimulus deprivation. |
|
|
30
|
The reader is reminded of
Guth's take on what the y-bar function is. It is the response of one
"second stage" subsystem within the visual system. The achromatic and
opponent systems combine vectorially. |
|
|
31
|
The unity or projection
operator is presented as a means to derive useful formulas. |
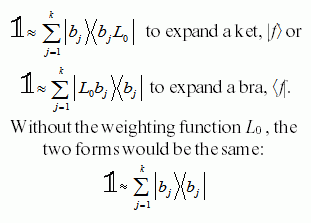 |
|
|
32
|
The unity operator that I
construct with orthonormalized basis functions equals Jozef Cohen's
Matrix R. Rather than emphasize the unity operator as a large square
matrix, I allow it to fade away in the derivation of the illuminant
substitution matrix. |
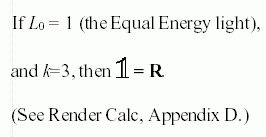 |
|