|
Effect
of Veiling Reflections on Vision of Colored Objects
James
A. Worthey
Introduction
Familiar light
sources vary by a factor of about 106 in the bright solid
angle they present. Table 1
ranks a number of sources according to the
solid angle subtended by their bright areas, based on simple
measurements and calculations. For instance, the filament area for the
unfrosted 60 W bulb is calculated from the observation that the coiled
coil appears to be 1 mm diameter by 20 mm long. For the ordinary
frosted lamp, naked-eye observation shows the bright spot to be a
circle of about 20 mm diameter. For the Soft White lamp, the bright
spot is taken to be a circle of the bulb diameter. Obviously, the
choice of 2 m distance for the individual electric lights is arbitrary
and affects their comparison with the sun and the luminous ceiling.
Nonetheless, the range of variation is great. (In Table 1, I forgo power-of-ten
notation for solid angles in order to dramatize the range of
magnitudes.)
Table
1---Light source sizes
|
Light
Source
|
Area,
(m2)
|
Solid
Angle at 2 meters distance, microsteradians
|
Unfrosted
60 W incandescent bulb
|
2.0×10-5
|
5
|
The
Sun (distance = 93 million mi)
|
1.5×1018
|
67
|
Ordinary
frosted 60-W incandescent bulb
|
3.1×10-4
|
79
|
Soft
White 60-W incandescent bulb
|
2.4×10-3
|
590
|
F40T12
fluorescent tube
|
4.6×10-2
|
12,000
|
Luminous
ceiling, extending to ∞ (2π steradians)
|
many
|
6,300,000
[2π million]
|
Light source area
has such an effect on highlight size and the abruptness of shadow edges
that the three incandescent types are sold side-by-side in US
supermarkets. A recent paper1 looked at two effects of light
source size: how larger sources make it more difficult to avoid veiling
reflections, and how source size affects the luminance of veiling
reflections. An important conclusion was that veiling reflections are
never negligible if they veil blacks and dark colors.
The three 4-percent
rules
An important set of conclusions in the earlier paper concerned the
amplitude of surface reflections. If a dielectric material is assumed
to have index of refraction n = 1.5, and light enters the material
approximately normal to the surface, then 4 percent of the incident
light will be reflected at the surface. For unpolarized incident light,
the reflected fraction remains approximately 4 percent up to about a 40
degree incident angle, then rises to 100 percent at grazing incidence.
For polarized light, other angles of incidence, and other refractive
indices, the reflected fraction is given by formulas found in Reference 1 or in elementary optics
books. Putting aside those complexities for the sake of a simplified
discussion gives us three "4-percent rules." To understand these rules,
picture a piece of black glass, which reflects only specularly, next to
a diffusely reflecting white surface. [Click for
a drawing.]
1) If light is incident more or less normal to an air-dielectric
interface, such as the black glass, about 4 percent will be reflected
at the surface.
2) If a source is imaged in a shiny dielectric surface, the
luminance of the veiling reflection (or highlight) is about 4 percent
of the source luminance.
3) Under spherical lighting (or a luminous ceiling extending to
infinity), the veiling reflection in the black glass is about 4 percent
of the luminance of the white surface next to it. (Since the white
surface has the same luminance as the spherical source.)
Veiling reflections
example
By extracting facts from that earlier paper, let us work an
illustrative example. Suppose that the visual task is a shiny book
whose half-width in its narrow dimension is 10.8 cm (4.25 inches).
Suppose that the light source is circular and oriented toward the book,
and that its angular semi-subtense (its angular "radius") is 27
degrees. Then if the source is 30 degrees off the line of sight (over
the shoulder), the book must be tipped about 7.5 degrees off the line
of sight and away from the light in order to avoid veiling reflections,
or a total of 37.5 degrees away from the light. This turning from the
light dims the book by (1 − cos37.5° ), or about 21
percent, without dimming the surround. Further calculations, taking
account of the non-linearity of human lightness perception, show that
if the reader does not tip the book and does not avoid the veiling
reflection, but allows it to wash out the blacks on the page, it
discards about half the dynamic range of black-white perception. The
calculations underlying this example are far from trivial, but were
handled by reading numbers off the graphs in the earlier paper.1
The present paper
extends the demonstration that veiling reflections are seldom
negligible. We shall examine the extent to which veiling reflections
reduce the saturation and diversity of colors seen in colored objects.
To do this, we must introduce some quantitative methods that are used
in talking about object colors.
The concept of a "color solid"
If a patch of light is created in a physics laboratory by a mixture of
red, green, and blue lights, then this light may be described by a set
of three numbers that may vary independently from 0 up to the limit of
radiant power available. If the three numbers are taken to comprise a
vector in cartesian space, then this vector can vary within a
rectangular parallelipiped bounded by the power limits—a simple
and perhaps not very interesting fact.
Now consider the
range of ordinary non-self-luminous objects, which are seen only by
reflected light. If the illuminant spectral power distribution (SPD) is
specified, then three numbers (called tristimulus values) can be
calculated, or measured, which describe the object as a stimulus to
color vision. This would be done by the ordinary methods of
colorimetry, and might lead to a luminance and chromaticity
(L, x, y),
for instance. If the illuminant is held fixed, the variation of the
triplet (L, x, y) is now limited by the condition that the
spectral
reflectance function of the object varies only between 0 and 1. This
limits (L, x, y) to a curved solid, the shape of which
expresses information concerning the light source, human vision, and
the constraint on spectral reflectance. This color solid expresses the
trade-offs involved in attempting to make pure colors with pigments; a
pigment can isolate one wavelength band only by absorbing other
wavelengths. It will have an irregular pyramid shape, indicating that a
saturated ("strong") pigment color will in general be a dark one; only
yellow pigments can be both light and saturated.
The most used color
solids incorporate additional facts, and are not pyramidal, but more of
an irregular football shape (North American football), small at the top
(the white end) and at the bottom (the black end). Because of lightness
constancy2 and color constancy,3 colors are
located in the solid based on their surface reflectance, rather than
their absolute radiance. A color's position in the color solid can be
calculated from its spectral reflectance. Position and distance within
the solid correspond approximately to human perception of colored
objects. From bottom to top through the solid is the axis of achromatic
colors: blacks, grays, and whites. On the surface are
the most saturated colors. The solid tapers toward black at the bottom
to represent the fact that dark colors appear less-than-fully
saturated, even if they reflect in just a narrow wavelength band. The
solid's shape shows that yellows can be saturated and high in
lightness, while the most saturated reds and blues are dark. The
calculation relating a surface color to a point within the solid is
nonlinear, corresponding to the nonlinear way that color differences
are perceived. The exact range of possible colors depends on the
spectral power distribution of the light that is assumed to illuminate
them. [To
see one color solid from all sides, go to Bruce Lindbloom's web site, http://www.brucelindbloom.com/
, then click "Info" and "Lab Gamut Display."]
If a standard light
source, such as Illuminant C, is considered to light the objects, then
the source SPD can be considered as background information and a color
solid can be taken to represent the boundaries of object color
perception by humans. Any realistic object spectral reflectance
function will map to a point within or on the surface of this solid,
and that point can be related to a color name, such as "dark red,"1
"pale blue," or to some appropriate set of three numbers that will
predict the object's color appearance. Descriptions of two such color
solids, apparently written by Dorothy Nickerson, appear in the American
Heritage Dictionary at the entry word color.4
The exception that proves the rule with respect to color solids is
fluorescent pigments. These violate the restriction that light radiated
cannot exceed light incident at each wavelength; and indeed the eye can
recognize this, that a fluorescent pigment displays a combination of
lightness and saturation which is outside the limits of normal pigments.
A
convenient color
space for calculation purposes is the CIELAB uniform color space.5
CIELAB maps any object color into three numbers L*, a*, and b*. L*
represents lightness, with L* = 100 representing white. Roughly
speaking, a* represents redness (if >0) or greenness (if <0)
while b* represents yellowness (if >0) or blueness (if <0). The
starting point for computing (L*,a*,b*) is usually (X,Y,Z)O
of the object, plus (X,Y,Z)W for a reference
white similarly lighted. The CIELAB calculation is invertible: given (X,Y,Z)W, (X,Y,Z)O
can readily be recovered from L*,a*,b*.
Effect of veiling
reflections on object color
The concept of a volume of possible colors provides a general way to
discuss lighting effects on color. Brill and Howland advanced the idea
of a volume-gamut index;6 Thornton and Chen have discussed
it in a general way7 and Xu has exploited it8 for
the purpose of describing color rendering effects, though Xu did not
use the term "volume." We now look at the effect of veiling reflections
on the limits of perceived object colors. Color rendering, meaning the
effects of the source SPD, is not a variable in this discussion. While
many discussions of color solids are based on the absolute mathematical
limits imposed by assuming spectral reflectance always less than one,9
we start with a different definition of the limits of the color solid.
Michael R. Pointer determined the limit of "real" surface colors by
making a search for examples of actual pigments displaying high
saturation. He started with the commercially available "Munsell Limit
Color Cascade," which is a set of 768 saturated color samples,10
and then extended this set with tabulated data and fresh measurements
of other colors, for a total of 4089 colors. From these, he mapped the
limits of the "real" color solid in CIELAB space (as well as another
color space, CIELUV), reporting the data in both graphical and tabular
form.10 The reference illuminant for all data was Illuminant
C. Pointer found it most revealing to deal with CIELAB space in a
cylindrical polar co-ordinate version. In this scheme, which is part of
the official definition of CIELAB,5 the axial coordinate is
L*, and the radius and hue angle (c*,h*) are the polar version of
(a*,b*). Thus, L* corresponds to the psychological dimension of
lightness; c*, the radial co-ordinate, corresponds to perceived
saturation of colors, and h* goes around the color circle, from red
(about 0 degrees) to yellow (about 90 degrees), green (about 180
degrees), through blue (about 270 degrees). Whites, grays, and blacks
of course lie along the L* axis (c*=0).
Pointer's data have the merit of realism, and it is actually much
easier to type them into a computer file than to write a program that
computes points on the theoretical extreme limits of the color solid.
The question was therefore asked, how much a given level of veiling
reflections would reduce the volume of Pointer's color solid in CIELAB
space, based on the desaturation and lightening that surface reflection
will cause. In accord with the data, the veiling light source was taken
to be Illuminant C. Veiling luminance was set to 4 percent, 8 percent,
12 percent, and 16 percent of the reference white. Results are
presented in Figure 1 for four of the 36 constant hue planes. The
effect of adding white to a particular color is shown by an arrow, with
its tail at the initial saturation (c*) and lightness (L*) and
arrowhead at the new values. Successive additions of 4 percent to each
limit color result in a chain of arrows. The first 4 percent represents
the veiling effect of spherical illumination.1 It will be
seen that this "small" admixture of white light causes a great loss in
the range of dark and saturated colors available, while it does add a
smaller amount to the range in the area of light colors of medium
saturation.
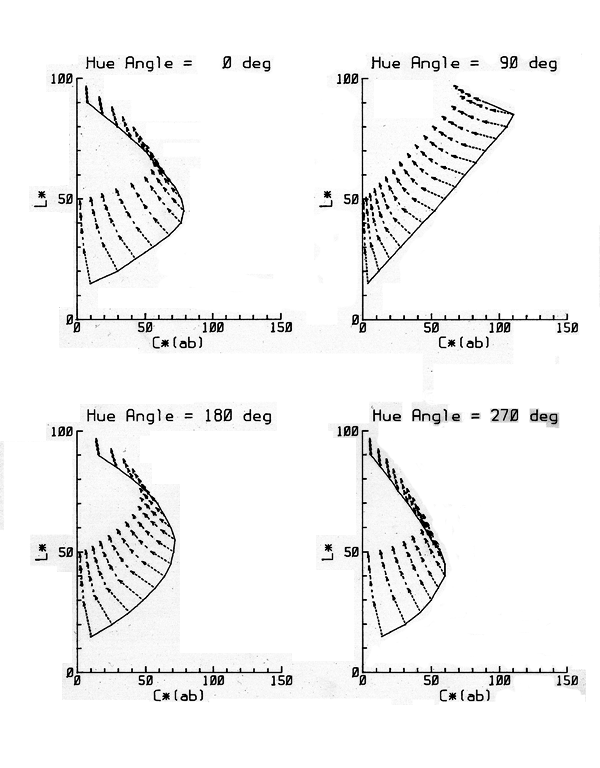
|
Figure 1—Reduction in the range of
lightness and saturation of surface colors due to veiling reflections.
Data are plotted in the cylindrical-polar version of the CIELAB uniform
color space, at four selected hue angles (h*). Radial coordinate c*
represents saturation, while axial coordinate L* is a measure of
lightness. The solid lines represent the limits attainable with real
pigments, according to Pointer.10 Chains of arrows show
successive shifts as veiling reflection
is increased to 4, 8, 12, and 16 percent of white. At these selected
hue angles, the shifts stay in the constant-hue plane, but at other h*
values, they don't. At all hue angles,
including those not shown, a similar systematic loss of saturation and
of lightness occurs.
|
Two effects are in evidence here. One is that as the white light is a
fixed color on the axis, its addition pulls all other colors toward the
middle, reducing their differences. This effect would show up in
virually any color space, and would always act to shrink the volume of
the solid. The other effect is not a purely physical one: it is that the
arrows at lower luminance levels are long, meaning that a vixed
increment of radiant power has a greater effect when added to a darker
color. This is the non-liearity of human vision that is expressed by
Munsell Value Scale, for instance.1 It is incoporated into
CIELAB in the form of a cube-root transformation.
Volume
of the color solid
The net effect of veiling reflections is to reducce the volume of the
color solid. The volume of a polyhedron determined by the limiting
colors was computed, based on the complete set of Pointer's data as
given at 10-degree increments in hue angle. (A slight ambiguity arises
in going from the set of points to a set of surfaces, which was
resolved by favoring local convexity. This minor technical decision is
expected to have little effect on the relative loss of volume as
veiling reflection is increased.)
Table 2
summarizes the results of the color-volume calculation. It shows that
spherical illumination, corresponding to 4 percent veiling reflection,
reduces the number of different colors that can be seen by 37 percent.
Sixteen percent veiling reflection, corresponding to the image of a
luminaire of 30° semi-subtense, will reduce the number of
colors by 72 percent.
Table
2. Volume of color solid as a function of veiling reflectance
|
Veiling
Reflection, as a Percent of White
|
Relative
Volume of Color Solid, as Percent
|
0%
|
100%
|
4
|
63
|
8
|
46
|
12
|
35
|
16
|
28
|
As pointed out in the earlier paper,1 giving a colored surface a
matte texture does not eliminate surface reflection but is similar to
making it shiny and then viewing it under spherical illumination. The
surface reflections are spread over a shemisphere. Thus, the 37 percent
reduction in number of colors gives an indication of why colored
pictures in particular are often given shiny surfaces. Of course,
photographic print papers cannot achieve the full gamut of colors that
Pointer spanned with many distinct pigments, so the 37 percent number
does not directly apply. But the fact that the use of three pigments
limits the color gamut of photographic papers10 is all the
more reason to conserve the remaining color solid by control of surface
reflections. The best control of surface reflections comes from giving
the surface a high gloss and then viewing the picture with a "light
trap"—a very dark surface—at the mirror angle.
The decrease in possible saturation of colors can be seen in the
differences between the matte and glossy sets of Munsell papers.
Munsell papers are a commercially available11 set of
color-painted papers based on the Munsell uniform color space.12,13
There are currently about 1600 notations exemplified in the glossy
finish collection but only 1300 in the matte finish collection. For numerous
technical reasons these numbers are not a direct measure of the volume
of glossy and matte color solids, but do give some clue as to the
practical loss of variety in matte colors. Since Munsell notation is
inherently a cylindrical system, similar to the cylindrical version of
CIELAB, the nature of the matte-glossy difference can be displayed in
diagrams at constant hue, similar to Figure
1. Figure 2 shows two
constant-hue slices through the set of available papers, with available
glossy papers denoted by rectangles.
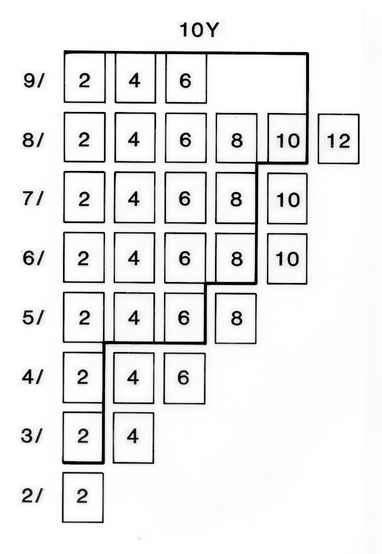
|
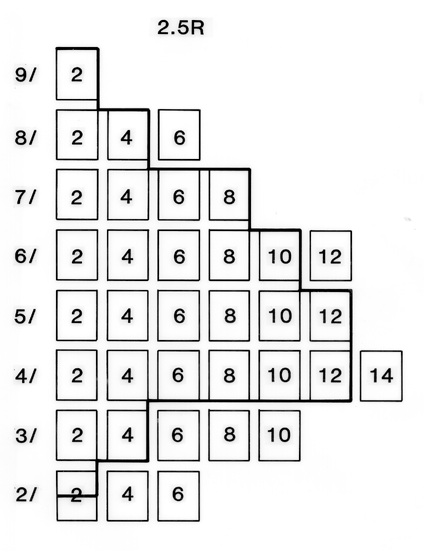
|
| Figure 2—Comparison
of the range of Munsell colors available in the glossy and matte sets.
Two constant-hue planes (10Y and 2.5R) are shown, similar to Figure 1. Rectangles with numbers
stand for glossy chips that are available. The heavy line indicates the
range of matte chips available. For instance matte chips are available,
but not glossy ones for notations 10Y9/8 and 10Y9/10. Glossy papers,
but not matte, are available for 10Y4/4 and 10Y4/y. |
For instance, the
rightmost rectangle in the top row under "10Y" indicates that there is (Figure 2) a glossy paper for
notation 10Y 9/6. (10Y indicates hue, a yellow; 9/ tells the Munsell
value; and 6 indicates chroma or saturation.) The heavy line encloses
those rectangles for which a matte paper is available. At hue 10Y, we
see that eight hues are lost, but two are gained in going from glossy
to matte. At hue 2.5R (a red), nine hues are lost and none are gained.
The solid line bisects the rectangle for 2.5R 2/2 to indicated that a
chip is sold at 2.5R 2.5/2. Where
possible, matte chips are made with the value 2.5, since none can be
made with value 2. In the neutral series, the pure whites, grays and
blacks, the glossy series goes down to value 0.5/, while the matte
series stops at 1.75/ on the black end.
Poor
man's anti-reflection coating
We may conclude that
a shiny surface is a poor man's anti-reflection coating. To use this
anti-reflection coating, the poor man must have a dark surface near his
light source that he can put at the specular angle.
Discussion
The loss of saturated colors due to veiling reflections compounds any
loss that is due to color rendering deficiencies of the light.14
For instance, Xu8 found that a Warm White fluorescent lamp
reduces the volume of accessible colors by 25 percent from its value
under Standard Illuminant A. Xu's concept of a color solid volume is
similar to that in the present paper, although his calculation differs
in important details.
Summary and conclusions
Light sources vary in the solid angle they subtend by a factor of
almost 106. A previous paper1 showed that veiling
reflections are easy to avoid if the source is small and has a dark
area next to it, but harder to avoid when the source is large. Because
of the nonlinear way that the eye perceives whites, grays, and blacks,
the bottom few percent of the reflectance scale is especially
important, and it was suggested in the earlier paper that veiling
reflections are not negligible, even under spherical lighting
conditions.
This paper has gone
further in showing why veiling reflections are not negligible. Dark and
saturated colors are particularly prone to being washed out by the
surface reflection of a light source. Spherical lighting, for instance,
reduces the range of possible colors by 37 percent, compared to
lighting with a compact source whose image can be moved off the page.
This is the net loss, with dark and strongly saturated colors being
lost, but a few lighter colors are gained.
Choosing a matte
finish rather than a shiny one is roughly equivalent to lighting the
shiny surface by spherical lighting. Shiny surfaces are used for
colored pictures and paints in order not to lose the "deep" colors.
This was emphasized by Figure 2,
which shows how the deep colors are lost from a set of paint chips, in
going from glossy to matte finish.
The conclusions
extend to lighting of three-dimensional objects. If a shiny colored
object is lighted by a compac source near a dark area, the source image
will be a bright white highlight, and the image of the dark area will
define a region in which the object's pigmentation can be clearly seen.
Acknowledgement
The author wishes to thank Dr. Michael H. Brill for writing the
subroutine used to calculate the volume of color solids. This work was
supported by the National Institute of Standards and Technology.
References
1. Worthey, J. A. 1989. Geometry
and amplitude of veiling reflections. J.
of the IES 19 (no.1).
2. Gilchrist, A.L. and Jacobson, A. 1983. Lightness constancy through a
veiling luminance. J. Exp. Psych:
Human Perception and Performance 9:936-944.
3. Worthey, J.A. 1985 Limitations of color constancy. Journal of the Optical Society of America
A 2:1014-1026.
4. Morris, W. Editor. 1978. The
American Heritage Dictionary of the English Language. Boston:
Houghton Mifflin.
5. Commission Internationale de L'Eclairage. 1978. Recommendations on
uniform color spaces, color-difference equations, and psychometric
color terms. Supplement No. 2 to CIE
Publ. 15 (E-1.3.1) 1971/(TC-1.3).
6. Brill, M.H. and Howland, B. 1976. Color gamut theory in the
assessment of lights and pigments. Mass.
Inst. of Technol. Res. Lab. of Electr Progress Reports, (no.
117):320-326.
7. Thornton, W.A. and Chen, E. 1978. What is visual clarity? J of the IES 7, 85-94.
8. Xu, H. Color-rendering capacity of illumination. 1983. J of the Optical Society of America.
73:1709-1713.
9. MacAdam, D.L. 1981. Color
Measurement: Theme and Variations. New York: Springer.
10. Pointer, M.R. 1980. The gamut of real surface colors. Color Res. Appl. 5:145-155.
11. Munsell Color Company, 2441 North Calvert Street, Baltimore, MD
21218, USA. [The address given is
historical. Munsell materials are sold by GretagMacbeth Corporation,
http://www.gretagmacbeth.com/
]
12. Wyszecki, G. and Stiles, W.S. 1967. Color Science Concepts and Methods,
Quantitative Data and Formulas. New York: John Wiley.
13. Newhall, S.M., Nickerson, D. and Judd, D.B. 1943. Final report of
the O.S.A. subcommittee on spacing of the Munsell colors. Journal of the Optical Society of America.
33:385-418.
14. Worthey, J.A., 1982. Opponent-colors approach to color rendering. J. Opt. Soc. Am. 72:74-82.
[Once again, this article
was
published in 1989: James A. Worthey "Effect of veiling
reflections on
vision of colored objects," Journal of the IES 18(2):10-15
(Summer 1989). The original has been
copied with a minimum of
editing. The text has been retyped, so there could
be typographical errors. Any inserted or updated material is in
[square brackets] or otherwise indicated. Jim
Worthey will welcome your comments.]
|