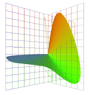
perspective view of locus Jim Worthey, Lighting and Color Research
home page contact about me
Jim Worthey • Lighting & Color Research • jim@jimworthey.com • 301-977-3551 • 11 Rye Court, Gaithersburg, MD 20878-1901, USA

Color Matching with Amplitude Not Left Out
Color Imaging Conference 12
Friday, 2004 Nov 12, 11:20 am
James A. Worthey, PE, PhD

Locus of  Unit Monochromats = The Eye's Vectorial Sensitivity to Color

Big Static Orthonormal Spectrum Locus



Talk Itself Starts Here

3 Main Ideas

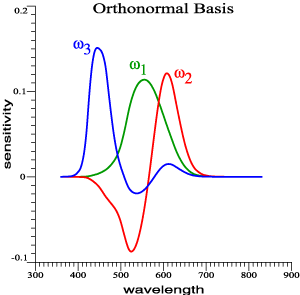
Orthonormal Basis
 Eye's Vectorial Sensitivity to Color
 Any Vectors
Orthonormal Color Matching Functions.
What's "Orthonormal?"
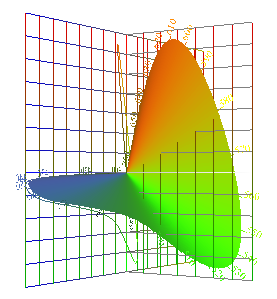
Vectorial Sensitivity to narrow-band lights.
Tristimulus vectors,
including amplitude.

Early Color-Matching Data of Guild or Wright.



Thoughts on Matching Data
The primary lights are not unique, and the same facts can be presented in alternate sets of graphs, an awkward situation. However,
  • Wright and Guild both used red, green, and blue primaries. The wavelengths are not really arbitrary.
  • The mixing of 3 primaries models technologies such as television.
  • Practical question: what wavelengths work best as primaries?

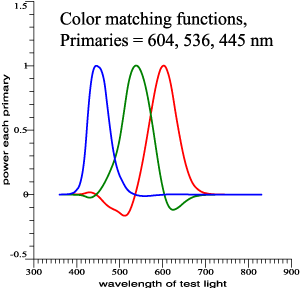
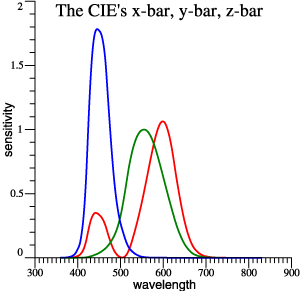
Same Color Matches, Varying Overlap among Functions:

Cone Sensitivities Color Matching Functions
 CIE's x-bar, y-bar, z-bar


(x, y) Diagram
So, we think in terms of the chromaticity diagram... 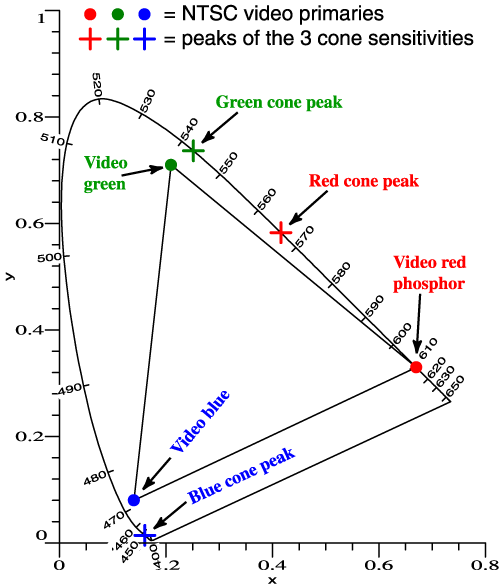video colors, cone sens. peaks but those primary colors are still needed.
Television dots.

Which Wavelengths Act Most Strongly in Mixtures?

MacAdam, and later Thornton did calculations like this.

Narrow-band lights of constant power are mixed with equal energy light. Some wavelengths perturb the white chromaticity more than others.

Thornton coined the term "Prime Colors" for the 3 wavelengths that act most strongly.

Color Matching Functions Are in Fact Relatively Stable
When the Primary Wavelengths Are Changed.

Later Thornton found:
  • The color matching functions tend to peak at certain fixed wavelengths, despite perturbation of the primaries.
  • The peaks occur at the prime colors.
  • Prime color primaries run the experiment at minimum power.
Michael Brill's new theorem:

When one primary wavelength is changed (say the red wavelength only) then the associated (red) color matching function changes only in scale, not in shape.

(For a more leisurely discussion of shifting primary wavelengths, please click here.)


Prime Colors Must Relate to the Overlap of Red and Green Sensitivities...
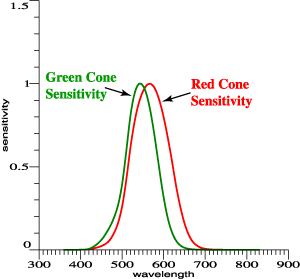
red, green cones
 red cone sensitivity minus green cone sens.
 ybar and an orthogonal function
Red and green cone functions are highly overlapping.
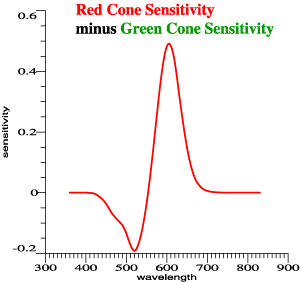
 Subtracting green from red gives peaks to account for Prime Colors, but the scaling is arbitrary.
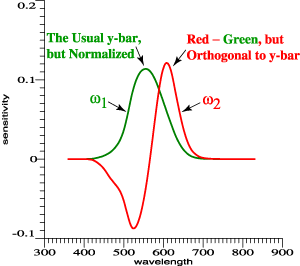
 Achromatic sensitivity, y-bar, is a linear combination of red and green. Find a second combination that is orthogonal to it.

One Degree of Freedom Remains, to Re-mix ω1 and ω2,
But Keep the Mixtures Orthogonal.

We start with ω1 and ω2, which are linear combinations of red and green cone functions, and are orthonormal. Other orthonormal pairs of functions can be generated by a rotation matrix: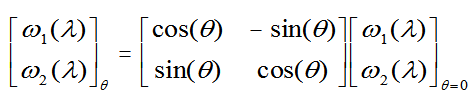


rotate by angle theta

Now Make a Parametric Plot of ω2 vs ω1.
Bingo, the Shape is Invariant.



Vectorial Sensitivity to Wavelength.
For each λ, the eye's sensitivity is a vector,
(ω2, ω1) .

 The spectrum locus is the eye's vectorial sensitivity to color. It is not a boundary.

The spectrum locus is alternatively the vectorial color of narrow-band lights, at unit power.
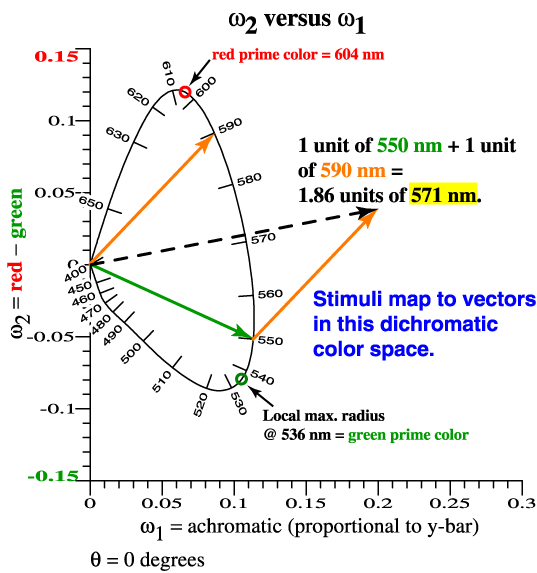 Vectorial addition of colors.
 Prime colors are the wavelengths where radius is a local maximum!

Stalking Prime Colors in the 2 Dimensions of Red and Green.
Progress so far:
  • Computing red minus green gives tentative prime colors---the plus and minus peaks of an opponent-color graph.
  • But, the peaks depend on the scaling of red and green, an arbitrary element.
  • Since achromatic sensitivity (y-bar) is a linear combination of red and green, find an opponent-color function that is orthogonal to y-bar.
  • Now we have a rationalized vector space for colors.
  • The prime colors---the wavelengths that act most strongly in mixtures---are the wavelengths that map to the longest vectors, 536 and  604 nm.
  • If we extend this method to include blue cones, then the spectrum locus in 3 dimensions is what Jozef Cohen called The Locus of Unit Monochromats. It is the eye's Vectorial Sensitivity to Wavelength. Cohen used different steps to reach this point.

Vectorial Sensitivity to Wavelength, Now in 3 Dimensions.
Orthonormal Basis
 Spectrum Locus in Orthonormal Space
Now include the blue cones to create a set of 3 orthonormal color matching functions.
 Combining the orthonormal functions into a parametric plot yields Jozef Cohen's "Locus of Unit Monochromats," the eye's Vectorial Sensitivity to Wavelength.

 Features of the Orthonormal System
  1. Axes have intuitive meanings: Achromatic, Red-Green, and Blue-Yellow.
  2. The first two functions, ω1(λ) and ω2(λ), combine red and green cones only.
  3. ω1(λ) is a multiple of the familiar y-bar.
  4. ω1(λ), ω2(λ) and ω3(λ) combine to give the eye's vectorial sensitivity to color.
  5. The functions are easily calculated, or get them from this link.
  6. A light's tristimulus vector has the same magnitude as the light's "fundamental metamer."
  7. Vector amplitude is non-arbitrary and has the units of the stimulus, such as radiance units. (Further explanation?)
  8. The mystery is now gone from Prime Colors. They are the red, green, and blue that map to the longest vectors. They are the wavelengths that act most strongly in mixtures, exactly as Thornton said.
  9. We don't usually learn to graph tristimulus vectors, or compute their magnitudes. Even graphs of the vector (X Y Z) would give some insight, but graphs and magnitudes mean more here.
  10. Algebraic benefit: orthonormal functions simplify derivations and formulas.
  11. Beginning students can be told flatly "This is the eye's vectorial sensitivity to color." Details can follow as needed.
Applications
Multi-primary, 8-color laser. xyz and cone sensitivities as vectors
Multi-Primary Imaging
  • Arrows from the origin show the 8 lines of a laser. They can be projected and modulated.
  • Vectors should be balanced and point in diverse directions.
  • Chained arrows (scaled down) sum to the tristimulus vector of the mixture.
Comparing Color Matching Functions
  • The orthonormal color matching functions map to the axes.
  • Other color matching functions, such as x-bar, y-bar, z-bar, or cone sensitivities plot as vectors.
  • Direction cosines are preserved, from wavelength space to this 3D space.

Color Rendering by Light Sources
Mercury Vapor, Daylight Spectra
 Mercury vapor light and daylight
A daylight phase has the same tristimulus vector as a certain high-pressure mercury vapor light.

[Sloppy calculation alert: The "daylight" is really outside the domain for the Judd, MacAdam, Wyszecki calculation.]
Color Rendering
  • Smooth chain is daylight decomposed into narrow bands.
  • The other chain---a commercial mercury light---takes a shortcut to white, because it is poor in reds and greens.

Oh, Yes, Calculating Tristimulus Vectors.
Inner product defined:
 inner product defined or similar.
Let L be a light, that is a Spectral Power Distribution.
Calculate XYX vector
 Calculate tristimulus vector in ortho basis.
Tristimulus vector found the old way.
 Tristimulus vector found the new way.
The calculation is essentially the same, but the benefits of the orthonormal color matching functions are tremendous!

Issues Demystified:
  1. What wavelengths make the best primaries in a color mixing experiment?
  2. Prime colors---wavelengths that act most strongly in mixtures.
  3. Television phosphors.
  4. Color rendering by lights. (This real-life issue is usually handled through hidden assumptions and arbitrary dogma.)
  5. Balance of primaries for multi-primary applications.
  6. Camera sensitivities, lighting for camera systems, etc. Examples have used the 2° observer, but the methods generalize.


Special Credit

William A. Thornton
Jozef B. Cohen

Michael H. Brill
Tom Cornsweet (1970 Book)
Ronald W. Everson (taught color fundamentals)
David MacAdam and Gershon Buchsbaum who mentioned orthogonal color matching functions.

(But MacAdam gets a demerit for disparaging Cohen's work.)

Calculations were done with O-matrix software.

Bill Thornton
William A. Thornton
Jozef B. Cohen
Jozef B. Cohen

Background
General Background, including Thornton's and Cohen's work is in
Render Asking: James A. Worthey, "Color rendering: asking the question," Color Research and Application 28(6):403-412, December 2003.

Mathematical detail is in
Render Calc:  James A. Worthey, "Color rendering: a calculation that estimates colorimetric shifts," Color Research and Application 29(1):43-56, February 2004.
See http://www.jimworthey.com  !

Seldom Asked Questions (links)

1. What Does "Orthonormal" Mean?

2. Why is the Tristimulus Vector the Best Measure of Stimulus Amplitude?

3. How Does the Orthonormal Basis Relate to Cohen's Matrix R?




Stop

Scroll No Farther
 Stop!
 Material Below Addresses Obscure Questions

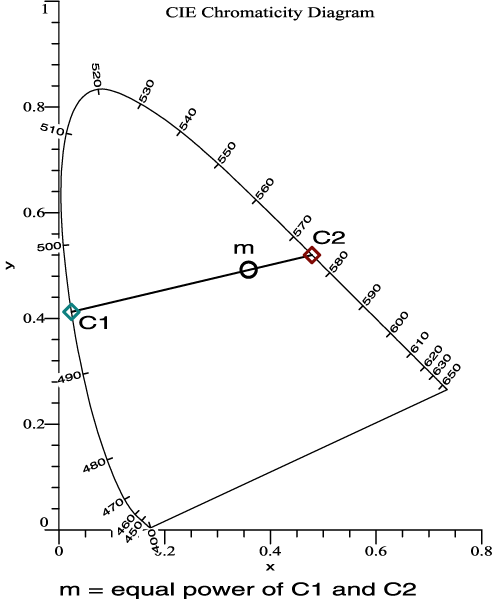
2 colors, C1 and C2 are set to equal power. The mixture is m.

Mixing of two colors at equal power




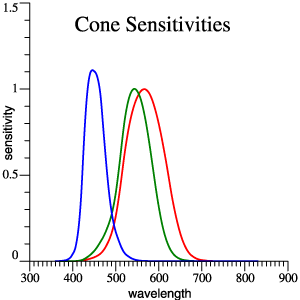
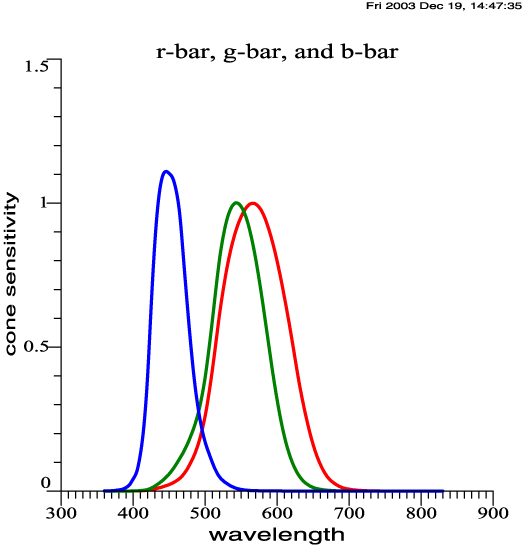
Cone Sensitivities, Approximately Smith-Pokorny Primaries
Cone sensitivity functions





Calculating the Guth Opponent Functions
define matrix M-zero
Columns of C are x-bar, etc
Compute matrix of opponent vectors



As a matrix of 3 columns,

G = [achromatic, red-green, blue-yellow]471 x 3




Guth's 1980 Model, Approximately

As a matrix of 3 columns,

G = [achromatic, red-green, blue-yellow]471 x 3

Opponent model of Guth, Massof & Benzschawel


Now Take Redundancy out of Guth's Model by Gram-Schmidt
big G to big Omega by Gram-Schmidt

inner products are Kronecker delta
big Omega in terms of little omega



Orthonormalized Opponent Functions
Orthonormal Basis = cmf's






Summary and Some New Issues
1. The initial stage of vision is linear and invariant.
2.  TV phosphor and autumn leaf need to act in the independent dimensions of color vision. Autumn leaf
 TV phosphor
3. Orthonormal color matching functions are as indpendent as possible.
4. Most arbitrariness drops out. One axis is whiteness.
5. No dispute with Jozef Cohen or Bill Thornton.

6. Some departure from Cohen's preferred treatment.
CIE says 471 numbers --> 3 numbers
But Cohen preferred the fundamental metamer as an invariant "color vector."
 471 numbers --> 471 numbers
With orthonormal basis, we can have it both ways. Equation (8)
N* squared
471 numbers --> 3 numbers
Tristimulus Vector is a Proxy for the Fundamental Metamer.

7. Color matching functions similar to raw data give an interesting spectrum locus, but X, Y, Z do not. See below.



Spectrum Locus for 4 Different Sets of Color Matching Functions
Locus in Orthonormal Space
Orthonormal Basis Functions
(Graph as Cohen drew it.)
 Locus based on narrow band primaries
Color Matching functions similar to
Raw Experimental Data
Locus based on cones r, g, b.
Cone sensitivities, r, g, b
 Locus based on x, y, z
CIE's x-bar, y-bar, z-bar





"Boomerang Graph," Not a Chromaticity Plot
Boomerang plot



Supplementary Material, Relationship to Jozef Cohen's Work

>>  Click Here



Copyright © 2004 James A. Worthey, email: jim@jimworthey.com
Page last modified, 2015 May 15, 00:12