Newton: In the late 1600s, Isaac Newton started a scientific revolution, for example by a new cause-and-effect understanding of planetary motion. Newton worked out his mechanics in one leap, and it is difficult to imagine it being otherwise. His laws of motion assume that friction is extraneous: "...a body in motion tends to remain in motion..." Very well, that almost makes sense, but he needed to take the next step and say "if I suppose frictionless motion and F=ma, what does that explain?" And then "suppose that planets move without friction." And then, "well, what keeps them on track? How about gravity?" To complete the picture, he wrote an algebraic law for gravity. Then, by the way, F=ma looks simple, but a is the second derivative of displacement with respect to time, so he had to invent calculus. He had to make a revolution. He couldn't make one timid advance at a time, really. He had to put all of his bold ideas on the table.
Let us now be bold and try to describe Newton's approach:
- Seek simple laws.
- Be bold. Don't cling to old
assumptions.
- Embrace math.
- Don't ignore simple examples. The
story of Newton and the apple tree is
probably true, but in any event it has logic.
The apple always falls toward the center of the earth.
Perhaps the earth's pull reaches the moon!
- Calculate some answers.
-
Let your concepts grow out of the simple laws and mathematics. Give precise meanings to words.
Another view is this. The time was ripe
for Newton's ideas, but suppose that he had not appeared
and a group of lesser minds had made his discoveries.
They would still be geniuses, but maybe two
mathematicians and two astronomers, reading each other's
work. They would have had an extended period of
uncertainty and controversy while they shared their
ideas. They would have needed an atmosphere of patience
and tolerance for uncertainty. Today, some scientists
enjoy such a climate, but others
do not.
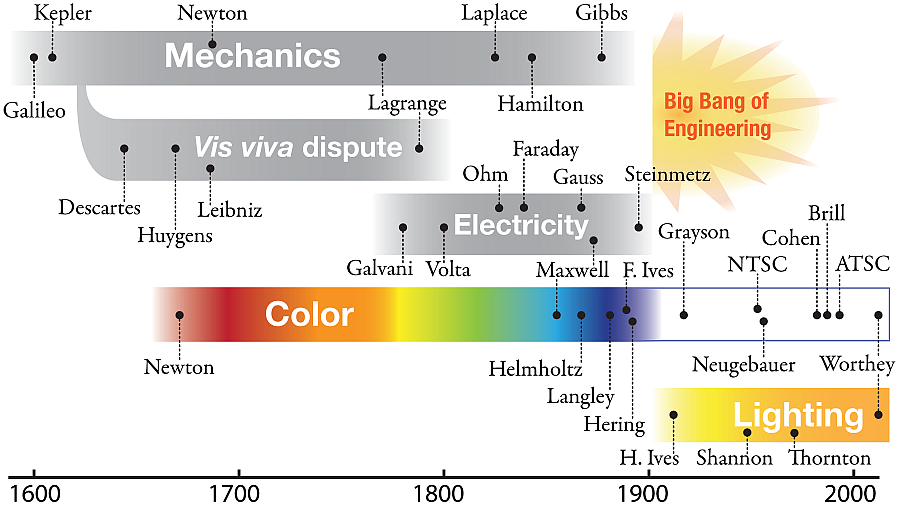
While 19th century ideas were a legacy for engineers to study and apply, physicists in the ragtime era were moving on. 1905 was Albert Einstein's Annus Mirabilis, in which he published 4 groundbreaking articles on the photoelectric effect, Brownian motion, special relativity, and mass-energy equivalence. That was the starting bell for a new era in which physics moved beyond the great discoveries of the 19th century.
So?? So engineers had what they needed, neatly packaged. That was all very well. They took their legacy for granted, as people do. But if we stop to think about the legacy, we notice:
- A simple idea in freshman physics is
that momentum, mv, is conserved. So is
kinetic energy, (1/2)mv2 . But
that's not really simple, it's confusing that the
two derived quantities are both conserved. It took
100 years of discussion to sort it out. See the "vis
viva" item below, a 2006 history of science article.
So, there was a 100-year
age of vis viva, or momentum and kinetic
energy.
- From Galvani's twitching frog legs to Maxwell's equations and Edison's first light bulb patent in 1880 was roughly a 100-year age of electricity.
- From Galileo to William Rowan Hamilton is roughly a 200-year age of mechanics. Add on a few decades for Heaviside and Gibbs to develop vector methods as they now appear in textbooks.
- From Newton to Maxwell and Helmholtz, count a 200-year age of color, from Newton's demonstrations and theory to the mature theory that Frederic Ives soon applied as a basis for color photography.
- In short, it takes extended
discussion by great minds so that a topic emerges
clear and simple and ready for the engineering
textbooks.
Now look for a creative period that
establishes the scientific understanding of lighting.
It has barely started. The traditional attitude is
mainly that light is good.
- Genesis Ch. 1, ver 3: "And God said,
Let there be light and there was light."
- Genesis Ch. 1, ver 16: "And God made two great lights; the greater light to rule the day, and the lesser light to rule the night: he made the stars also."
So, light is good, and there are
different kinds of light. That is very well. Artists
might begin to notice more, how lighting conditions
vary and how light interacts with objects. To
take us toward scientific understanding, we have
little legacy from ancient times, or from Galileo or
Newton, or even Maxwell. To begin to
understand lighting, we require the whole package of
classical physics, from Newton's insight that white
light is (usually) a mixture of all colors, to the
laws of optics, and the methods of radiometry and
photometry, plus some modern understanding of topics
like color mixture. Late innovations to enable
calibrated optical measurements were Grayson's ruling
engine for diffraction gratings, described in a 1917
publication, and work, including by Langley, on
measurement of optical power. (See below.)
 |
|
|
Daylight is variable, but on a sunny day it comprises the rays from the sun's disk plus light from the rest of the sky dome. The sun covers only about 10-5 of the sky dome. ["Lighting quality and light source size," Journal of the IES 19(2):142-148 (Summer 1990). Web version.] Before electric lighting, artificial lights were flames: campfires, candles, oil lamps and so forth. At right is an interior view of Charles P. Steinmetz's summer cabin, showing among other things a kerosene lamp. (The cabin is preserved in a museum. The photo was taken by Nicholas J. Worthey in 2004.)
Then in the age of flame lighting, what did Edison invent? An incandescent lamp, with a filament that was relatively bright and compact and had the color of a flame. With present knowledge we can confirm that the filament was an approximate blackbody radiator and indeed had a spectrum similar to that from a flame. Edison probably understood as much--took it for granted.
In short, incandescent lights were a small step away from the world of flames for lighting. In the year 1912, a person could be an illuminating engineer, but he had mainly one source to work with. The engineering had to do with
- The size and number of incandescent bulbs,
- and where to put them,
- and how to wire them up,
- plus the design of glass globes and lenses.
 |
|
|
The true illumination engineering lies in the steps that go beyond electricity and wiring: positioning the lamps and designing lenses, reflectors and the sources themselves. Electricity can power not only carbon arcs and filaments, but other lights which do not mimic flames at all. Before vapor discharge lamps were common, it was understood how strange they could be. US Patent 1025932, granted to C. P. Steinmetz in 1912 explains: "Hence it appears that an arc between electrodes, at least one. of which is formed of mercury, should be an extremely efficient light-giving arrangement, and this is indeed the fact, but the mercury arc is, unfortunately, of an extremely disagreeable color., It gives a discontinuous spectrum containing the Fraunhoefer lines 4047; 4359; 5461; 5769 and 5790, and some fainter intermediate lines. The sodium line, 5890, sometimes appears faintly, but this is probably due to the action of the glass or the presence of some impurity."
A scientific approach would give some thought to idiosyncratic lights, even hypothetical ones, and how they might affect vision of objects. Herbert Ives's passing remark in a 1912 article, discussed at right, calls our attention to a uniquely strange hypothetical light, a white light that comprises just two narrow bands, a blue and a yellow.
Ives's example was hypothetical but not impossible and its strangeness is echoed in 20th century technologies such as high-pressure mercury vapor lights, and even everyday fluorescent lights.
What does not live on is Ives's spirit of inquiry. His example, a kind of ideally bad light, does not speak to the physics of plasma discharges, but to the way the eye has evolved, with highly overlapping sensitivities in the red and green receptors. By the logic of the two-bands example, our vision of red-green object contrasts is uniquely at risk. But discussions of lighting and color seldom deal with these facts.
The two-band light is an extreme example for lighting and color. For the issue of light source size and placement, an extreme example would be that an object is lighted from all sides, as when it is in an integrating sphere. The discussion can then easily move to examples of compact sources (with small area) and the range in between. Other issues would call for other extreme examples.
A scientific approach would explore the cause-and-effect meaning of each issue and its extreme possibilities. In the 20th century, there was a problem that hypothetical sources remained hypothetical. It was not possible, on a reasonable budget, to build an apparatus that allowed an experimenter to manipulate a parameter such as light source spectrum in a systematic way. The exception that proved the rule was Edwin Land's experiments with projectors, cited at right. The experiments stood out in that the experimenter could turn knobs and adjust the lights. It appears that the setups used considerable lab space and some money, but for a lighting experiment (rather than the interesting experiment that was done), even more projectors might be needed. (For readers who are not native speakers of English: "the exception that proves the rule" is an old expression meaning an exception or extreme case that tests a rule.) In principle, Land showed the way to new lighting experiments, but the apparatus was cumbersome and nobody extended his method to other kinds of experiments.
To learn more about the experiments with projectors as light sources, see http://mccannimaging.com/Retinex/Home.html , then visit the topics Color, Retinex, and Color Constancy .
21st century technology, especially LEDs, will give new possibilities for systematic experiments. It will still take some money and electronics skills.
| Return to Top | Skip
to Bottom |
- A Letter of Mr. Isaac Newton, Professor of the Mathematicks in the University of Cambridge; Containing His New Theory about Light and Colors: Sent by the Author to the Publisher from Cambridge, Febr. 6. 1671/72; In Order to be Communicated to the R. Society. Isaac Newton, Phil. Trans. 1671 6, 3075-3087 , doi: 10.1098/rstl.1671.0072 (Available from Jim W. or by searching on the doi. Wikimedia version.)
- Principia Mathematica - 1687
On 2015 Feb 18, Google published this animation to celebrate Volta's 270th birthday:

"Pierre-Simon, marquis de Laplace (/ləˈplɑːs/; French: [pjɛʁ simɔ̃ laplas]; 23 March 1749 – 5 March 1827) was a French mathematician and astronomer whose work was pivotal to the development of mathematical astronomy and statistics. He summarized and extended the work of his predecessors in his five-volume Mécanique Céleste (Celestial Mechanics) (1799–1825). This work translated the geometric study of classical mechanics to one based on calculus, opening up a broader range of problems. In statistics, the Bayesian interpretation of probability was developed mainly by Laplace.[2]
Laplace formulated Laplace's equation, and pioneered the Laplace transform which appears in many branches of mathematical physics, a field that he took a leading role in forming. The Laplacian differential operator, widely used in mathematics, is also named after him. He restated and developed the nebular hypothesis of the origin of the solar system and was one of the first scientists to postulate the existence of black holes and the notion of gravitational collapse."
In 1839, he completed a series of experiments aimed at investigating the fundamental nature of electricity; "
On the science of the eye and vision, "His main publication, entitled Handbuch der Physiologischen Optik (Handbook of Physiological Optics or Treatise on Physiological Optics), provided empirical theories on depth perception, color vision, and motion perception, and became the fundamental reference work in his field during the second half of the nineteenth century." [Wikipedia, article on Helmholtz, section entitled 'Ophthalmic optics.']
- James Clerk Maxwell, “Experiments on
Colour, as Perceived by the Eye, with
Remarks on Colour Blindness,” Transactions of the Royal Society of Edinburgh, Vol. XXI, Part II, 275-298 (1855). http://www.jimworthey.com/archive/index.html - James Clerk Maxwell, A Treatise on
Electricity and Magnetism, Oxford: Clarendon
Press, 1873. (2
volumes.)
Notice that even Maxwell's mathematical
formulation of electricity and magnetism can be
construed as an elaboration of earlier work by Faraday
and others. The modern presentation of Maxwell's
Equations as a set of 4 formulas in alternate
forms is itself an extension of Maxwell's original
treatise.
Many sources (such as Wikipedia) may emphasize the dispute between Hering's opponent color theory and that of Thomas Young, James Clerk Maxwell, and Hermann von Helmholtz, who emphasized 3 primary colors, red, green and blue. The Wikipedia article on Hering says "But nowadays we know that if the human possesses indeed 3 types of receptors as proposed by Young, Maxwell and Helmholtz they are then combined in 3 opponent channels as proposed by Hering. In their way both Hering and Helmholtz were right."
Wikipedia is correct that both Hering and Helmholtz were right. In this case, I (James Worthey) suggest that opponent colors is a bedrock idea that fits various kinds of evidence:
- Intuitively, if you begin to name simple colors, you may easily notice an orange that is intermediate between yellow and red, or a yellow-green that is intermediate between yellow and green and so forth. But you will not observe a greenish red or a yellowish blue. It is intrinsic in the eye's function that blue and yellow are opposites, with white in the middle. Also red and green are opposites, with yellow or white in the middle.
- Physiologists find red-green opponent cells within visual systems, and the processing from RGB to the opponent system takes place right in the retina. [David H. Hubel, Eye, brain, and vision, New York: Scientific American Library, 1968; paperback edition 1995. The book is now available on the web: http://hubel.med.harvard.edu/book/bcontex.htm .] [Webvision, The organization of the Retina and Visual System, edited by Helga Kolb, Eduardo Fernandez, and Ralph Nelson, Salt Lake City (UT): University of Utah Health Sciences Center; 1995-. Available on the web: http://www.ncbi.nlm.nih.gov/books/NBK11530/ ]
- Sherman Lee Guth used opponent models
to explain various results. [For example, Guth,
Sherman Lee, Robert W. Massof, and Terry Benzschawel,
“Vector model for normal and dichromatic color
vision,” J. Opt. Soc. Am. 70, 197-212
(1980).] Also, there were experiments published
beginning in the 1970s described as Minimally Distinct
Border Experiments which are explained by
opponent-colors.
- The NTSC color television system from
1953 was based on an assumption about opponent
processing in the eye, and also used an opponent
principle in the way that color was encoded on the
radio waves.
- Since the overlapping red and green signals are correlated, it makes better use of bandwidth in the optic nerve to convert the cone signals to an opponent system. [Gershon Buchsbaum and A. Gottschalk, “Trichromacy, opponent colours coding and optimum colour information transmission in the retina,” Proc. R. Soc. Lond. B 220, 89-113 (1983).]
- With a stated goal of understanding
such ideas as Thornton's prime colors, plus some
mathematical ideas, I derived an orthonormal opponent
color system that is essentially the same result as
that of Buchsbaum and Gottschalk, just cited. This
system is then an aid to understanding and
problem-solving. [James A. Worthey, "Vectorial color,"
Color Research and
Application, 37(6):394-409 (December 2012).
http://onlinelibrary.wiley.com/doi/10.1002/col.20724/abstract] [Or, a preprint is at http://www.jimworthey.com/vectorial.pdf ; be sure to download the figures: http://www.jimworthey.com/vectorialfigs.pdf ]
Looking at Steinmetz's contributions to AC circuit theory, we can say that the ideas were inevitable. For example, consider a capacitor (called a condenser in Steinmetz's day I believe) as an element in a circuit. Physics teaches that the current is proportional to the time derivative of voltage, I = C dV/dt . If applied voltage is a sinusoid, then you may write something like V = V0 sin(2πft) and I = 2πfCV0 cos(2πft) and so forth. The current is out of phase from the voltage. The current through a resistor is in phase with the voltage, and then if you add those currents you are adding a sine and a cosine with different amplitudes and some kind of trigonometric identity comes into play. An engineer would notice that he is doing much tedious algebra with great similarities from one problem to the next. Steinmetz realized that the repetitive steps could be written more easily and compactly using complex numbers. In effect, sine and cosine waves add as perpendicular vectors, while differentiation reduces to complex multiplication, and so forth. Because he worked quickly and wrote actual textbooks, his ideas must have gone in a short time from being unexpected and odd to being the iron-clad rules of self-confident engineers. History tends to celebrate tangible gadgets and not the books that the inventor read or wrote. However, it does appear that Steinmetz showed up at the right moment and was a smashing success as a textbook author, among his other accomplishments.
Steinmetz's writings covered DC and AC machines and more. I emphasize AC circuit theory to show how 20th century engineering came to be. By 1900, physics reached a plateau of completeness, a basis for design and analysis of practical machinery. Then a transition was needed, to take from physics a subset of ideas that can be applied again and again to analyze practical systems. In the electrical realm, Charles Proteus Steinmetz personified that transition and what it means to create a body of practical methods based on valid science.
- Ives, Frederic E., A new principle in heliochromy, Philadelphia: Printed by the author, 1889.
- Ives, Frederick E., “The optics of trichromatic photography,” Photographic Journal 40, 99-121 (1900).
These writings are available by searching
on the web, or by contacting James Worthey.
In the book, item 1, Ives explains "This
principle may be conveniently stated as that of
producing sets of heliochromic negatives by the action
of light rays in proportion as they affect the sets of
nerve fibrils in the eye, and images or prints from
such negatives with colors which represent the primary
color sensations."
That statement, and the detailed
explanation that goes along with it, lays out an idea
that now can be called "The Maxwell-Ives Criterion."
Today we see have the concepts of block diagrams and
linear algebra, so a modern statement is Michael Brill's
formulation:
Maxwell-Ives Criterion: The camera sensitivities
should be linear transformations of those for the
retinal cones.
- The photoelectric effect,
- Brownian motion,
- Special relativity, and
- Mass-energy equivalence.
Transactions of the IES, Volume 7, is available on Archive.org as one big file. Click the link above to download it. You will have 3 articles by Herbert E. Ives and other writings which reveal how lighting was understood, or not, 100+ years ago.
- "The relation between the color of the illuminant and the color of the illuminated object," p. 62-72.
- "Heterochromatic photometry, and the primary standard of light," pp. 376-387.
The first article is on the topic that we
might call "lighting and color," or "color rendering,"
although Ives's title is clear in itself. In that
article he observed "It is, for instance, easily possible
to make a subjective white, as by a mixture of
monochromatic yellow and blue light. A white surface
under this would look as it does under "daylight" but
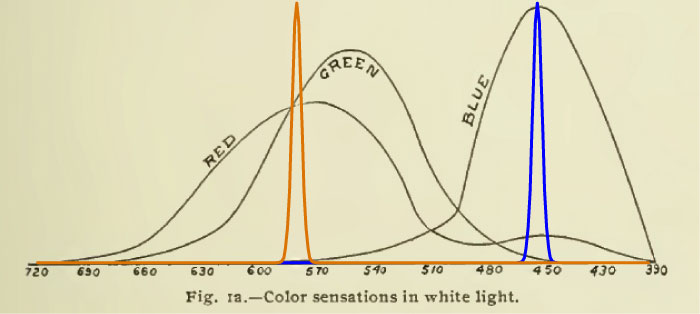
hardly a single other color would." Although Ives does not
explain at length, he supplies a graph. We can assume
that the monochromatic blue is at about 450 nm, and the yellow
is at about 580.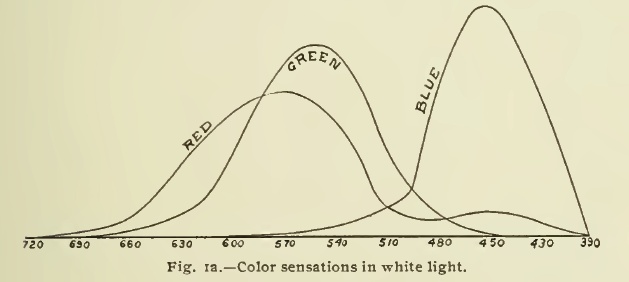 See below, near
the end of this timeline, how Thornton and Chen in 1978 revived Herbert
Ives's 1912 idea of
a white light that comprises a blue narrow band plus a
yellow narrow band. Worthey drew the connection of the
Thornton and Chen work to that of Ives. [James A. Worthey,
"Limitations of color constancy," J. Opt. Soc. Am. A
2, 1014-1026 (1985). ]
See below, near
the end of this timeline, how Thornton and Chen in 1978 revived Herbert
Ives's 1912 idea of
a white light that comprises a blue narrow band plus a
yellow narrow band. Worthey drew the connection of the
Thornton and Chen work to that of Ives. [James A. Worthey,
"Limitations of color constancy," J. Opt. Soc. Am. A
2, 1014-1026 (1985). ]
Now, let us lay in the narrow bands that Ives
described, "a mixture of monochromatic yellow and
blue light."
This shows what Ives described but did not draw:

The two narrow bands are at 450 nm and 580
nm. The problem is, if you look at the graph, that the
yellow light stimulates both the red-sensitive and the
green-sensitive receptors. This two-bands light can be
"daylight" color--a shade of white. Depending what shade
of daylight you want to match, the amplitude and
wavelength of the yellow band can be adjusted to refine
the match. But the range of colored objects from red to
yellow to green differ in how they reflect red, green
and yellow light.
 (Photo from
Wikipedia.)
(Photo from
Wikipedia.)Red, yellow and green hues will not be distinguished if the light contains narrow-band yellow, but no red and no green. Herbert Ives was pointing out, in 1912, the issue that leads to "color rendering" problems, however you want to say it. And where did he publish this insight? In the Transactions of the Illuminating Engineering Society, the predecessor publication to the Journal of the IESNA, still put out by the same society. Of course the famous color-rendering document was first published by the CIE (Commission Internationale de L'Eclairage) in 1965. Did they acknowledge Ives's insight? No, not then and not now. Thornton and Chen called attention to the issue in 1978 (citation below). Worthey first used opponent colors as an approach to the same issue in 1982 (citation below). Opponent-colors thinking led to Vectorial Color. (Citations below.)
Vectorial Color is the answer to more than one problem, but look at the figure above, where narrow bands at 450 and 580 nanometers were laid into Ives's drawing. 580 is indeed yellow. Also in the drawing it is roughly the wavelength where the red and green sensitivities cross. That emphasizes that it stimulates both systems, so it "makes sense." But the point where those functions cross depends on the scale of the functions, so it's arbitrary. In his work under the heading of "Matrix R," Jozef Cohen revealed a deeper truth about color mixing that does not depend on the way the sensitivities are scaled, or added and subtracted. Vectorial color combines Cohen's insights with the opponent-color formulation.
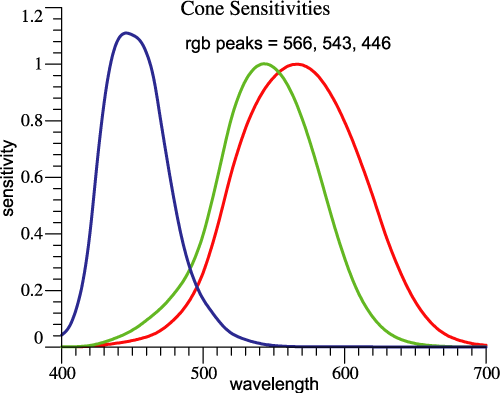
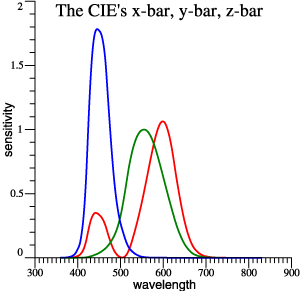
At left are the red, green, and blue receptor sensitivities based on the CIE 1931 observer. We can imagine a 2-bands light drawn in here, again at 450 and 580 nm.
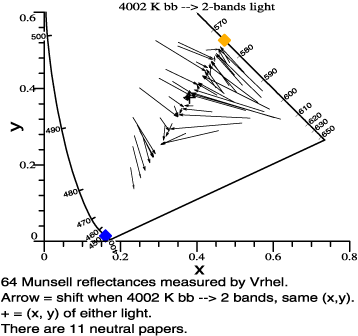
At left is a self-explanatory figure based on the (x, y) diagram and a 2-bands light slightly different from the one above.
Notice that lightmeter sensitivity, the y-bar function graphed below, is near its peak at yellow wavelengths of 570 to 580. So Ives's example is one that cheats on an illuminance requirement. It stimulates the lightmeter but deprives the user of red-green contrasts. Ives did not give a practical example, but fluorescent lamps (introduced about 1939) do this exact thing, presenting a 2-band spectrum, but with a broad yellow band so that red-green contrasts are not totally eliminated.
So that's color rendering. Traditional 4-foot or 8-foot fluorescent tubes have another failing. That is, the surface luminance is much lower than the luminance of a tungsten filament. The lower luminance source has a greater area, causing loss of shading, shadows and highlights, and converting the highlights to veiling reflections. Traditional fluorescent lights do everything wrong at once.
"Heterochromatic photometry, and the primary standard of light," pp. 376-387.
- http://www3.alcatel-lucent.com/bstj/vol27-1948/articles/bstj27-3-379.pdf
- http://www3.alcatel-lucent.com/bstj/vol27-1948/articles/bstj27-4-623.pdf
However, an updated and reformatted
version is linked at: http://cm.bell-labs.com/cm/ms/what/shannonday/paper.html
James Gleick's book The Information,
cited below, puts information theory in context and
explains its importance. Imaging, lighting, and vision
itself are about the transmission of information.
Contrasts are the stimulus to vision.
- Complex numbers add as 2-vectors, but have their own form of multiplication.
- The inner product (dot product) is defined for 2-vectors, 3-vectors, or any dimension. But the result is a scalar, not a vector.
- Cross product c = a×b gives a vector c perpendicular to the plane of a and b, so it is specifically a method for 3-space.
- To write Maxwell's equations and other physics, we need those special symbols for vectorial partial derivatives. Those compact notations an innovation not available to Maxwell himself.
- Rotation matrices work well for certain problems. To rotate objects in computer graphics, we need William Rowan Hamilton's quaternions.
Crowe's book reveals the struggles
leading to this intricate schema. See a
summary.
- Jozef B. Cohen, “Dependency of the spectral reflectance curves of the Munsell color chips,” Psychonom. Sci. 1, 369-370 (1964).
- Cohen, Jozef and T. P. Friden, “Euclidean color space and its invariants,” Proceedings of the Technical Association of the Graphic Arts, 411-429 (1976).
- Jozef B. Cohen and William E. Kappauf,
“Metameric color stimuli, fundamental
metamers, and Wyszecki’s metameric blacks,” Am. J. Psych. 95(4):537-564 (1982).
- Jozef B. Cohen and William E. Kappauf, “Color mixture and fundamental metamers: Theory, algebra, geometry, application,” Am. J. Psych. 98(2):171-259, Summer 1985.
- Jozef B. Cohen, Visual Color and
Color Mixture: The Fundamental Color Space,
University of Illinois Press, Champaign, Illinois, 2001, 248 pp.
- William A. Thornton, “Luminosity and color-rendering capability of white light,” J. Opt. Soc. Am. 61(9):1155-1163 (September 1971).
- Haft, H. H., and William A. Thornton,
“High performance fluorescent lamps,” J. Illum. Eng. Soc.,
2(1):29-35, October 1972.
- William A. Thornton, “Three-color
visual response,” J. Opt. Soc. Am. 62(3):457-
459 (1972). - Thornton, William A. and E. Chen, “What is visual clarity?” J. Illum. Eng. Soc. 7(2):85-94 (January 1978).
- William A. Thornton, “A simple picture of matching lights,” J. Illum. Eng. Soc. 8(2):78-85 (1979).
- Michael H. Brill, Graham D. Finlayson, Paul M. Hubel, William A. Thornton, “Prime Colors and Color Imaging,” Sixth Color Imaging Conference: Color Science, Systems and Applications, Nov. 17-20, 1998, Scottsdale, Arizona, USA. Publ. IS&T, Springfield, Virginia.
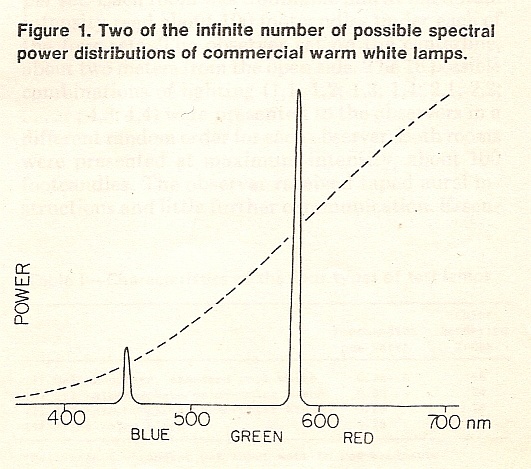
In the 4th item, “What
is visual clarity?” Thornton and Chen revive Herbert
Ives's suggestion (above) that a specified white can be
matched by a mixture of 2 narrow bands. Their Fig. 1:
1990s
See the discussion above on the 1953 NTSC standard. The newer standards for high-definition TV are another reference point for thinking about analytical methods and what works for humans. Television standards are about delivering visual stimuli to users. "High Definition" implies high black-white and color contrasts (as appropriate to the original scene) with sharp edges.
Lighting systems control black-white and color contrasts that potentially exist in a scene. Lighting that pleases users will imbue a scene with the same virtues that are valued in high-definition video. In a way that is obvious and has been understood for decades. However
-
“Near the end of 1668, ... John Wallis (1616–1703) and Christopher Wren (1632– 1723), submitted papers to the Royal Society presenting rules of impact.10 ” - “Leibniz provoked the vis viva controversy in stages, beginning in 1686 and culminating in 1695.”
James
A. Worthey, "Vectorial color," Color Research and Application, 37(6):394-409
(December 2012).
http://onlinelibrary.wiley.com/doi/10.1002/col.20724/abstract
James
A. Worthey, "Applications of vectorial color," Color Research and
Application, 37(6):410-423 (December 2012).
http://onlinelibrary.wiley.com/doi/10.1002/col.20723/abstract
- Michael Brill, Gerhard West,
"Contributions to the theory of invariance of color
under the condition of varying illumination," Journal
of Mathematical Biology 11(3):337-350, March
1981.
- Michael H. Brill, "Decomposition of Cohen's matrix R into simpler color invariants," American Journal of Psychology 98(4):625-634, Winter 1985.
- Michael H. Brill and Henry
Hemmendinger, "Illuminant dependence of object-color
ordering," Die Farbe 32/33 (1985/6),
35-42.
- Michael H. Brill, Letter to the Editor
of CR&A concerning a formal analogue to the
spectrum locus based on the principal components in
Cohen's 1964 article, Color Research and
Application 12(4):226-227, August 1987.
- Michael H. Brill, "Image segmentation
by object color: a unifying framework and connection
to color constancy," J. Opt. Soc. Am. A 7(10):2041-2047,
1990.
- Hugh S. Fairman, Michael H. Brill, Henry Hemmendinger,"How the CIE 1931 Color-Matching Functions Were Derived from Wright–Guild Data," Color Research and Application 22(1):11-23, February 1997.
- Michael H. Brill, Erratum to the article just cited, Color Research and Application 23(4):259, August 1998.
- Michael H. Brill, "Color science applications of the Binet-Cauchy theorem," Color Research and Application 27(5):310-315, October 2002.
- Hugh S. Fairman and Michael H. Brill, "The principal components of reflectances," Color Research and Application 29(2):104-110, April 2004.
- Michael H. Brill and James Larimer,
"Avoiding on-screen metamerism in N-primary
displays," Journal of the Society for Information
Display 13(6)509-516, June 2005.
Michael took responsibility for the final
editing of Jozef B. Cohen's book, Visual Color and
Color Mixture, published posthumously. See above.
Johnston notes (at length) the peculiar beginnings of the profession of Illumination Engineering. The initial challenge was to quantify light. In the preface, p. ix: "The measurement of brightness came to be invested with several purposes. It gained sporadic attention through the 18th century. Adopted alternately by astronomers and for the utilitarian needs of the gas lighting industry from the second half of the 19th century, it was appropriated by the nascent electric lighting industry to ‘prove’ the superiority of their technology. By the turn of the century the illuminating engineering movement was becoming an organized, if eclectic, community promoting research into the measurement of light intensity."
We found Bowmaker's interesting article free of charge: http://www.sciencedirect.com/science/article/pii/S004269890800148X . Our search began with the powerful PubMed online index: http://www.ncbi.nlm.nih.gov/pubmed . PubMed indexes materials that are free and ones that are not free, but many interesting items are free.
There is a free textbook called Webvision that is hosted by National Library of Medicine and also by University of Utah:
http://www.ncbi.nlm.nih.gov/books/NBK11530/ or http://webvision.med.utah.edu/ .
In Webvision, the emphasis is on anatomy, but some other topics are included.
